练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数上的最大值和最小值之差为,则值为（　  ）

        ﹙A﹚  2或       ﹙B﹚ 2或4        ﹙C﹚ 或4         ﹙D﹚ 2

    A    

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）对于任意x，y∈R总有f（x+y）=f（x）+f（y），且当x＞0时，f（x）＜0，f（1）=-
    23
    ，
    （1）求证：f（x）是R上的奇函数．
    （2）求证f（x）在R上是减函数．
    （3）求f（x）在[-3，3]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=4x2-4ax+a2-2a+2
    （1）当a=0时，求f（x）=4x2-4ax+a2-2a+2在区间[0，2]上的最大值和最小值．
    （2）若函数f（x）=4x2-4ax+a2-2a+2在区间[0，2]上的最小值为3，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

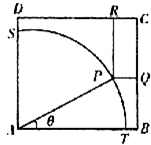    随着机动车数量的增加，对停车场所的需求越来越大，如图，ABCD是一块边长为100米的正方形地皮，其中ATPS是一座半径为90米的扇形小山，P是弧TS上一点，其余部分都是平地，现一开发商想在平地上建一个边落在BC和CD上的长方形停车场PQCR．
    （1）设∠PAB=θ，试写出停车场PQCR的面积S与θ的函数关系式；
    （2）求长方形停车场PQCR面积的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•盐城二模）设函数fn(x)=-xn+3ax+b（n∈N*，a，b∈R）．
    （1）若a=b=1，求f3（x）在[0，2]上的最大值和最小值；
    （2）若对任意x1，x2∈[-1，1]，都有|f3（x1）-f3（x2）|≤1，求a的取值范围；
    （3）若|f4（x）|在[-1，1]上的最大值为
    12
    ，求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数

    （1）将函数化简成的形式，并指出的周期；

    （2）求函数上的最大值和最小值.

    查看答案和解析>>

    同步练习册答案