
分析 (Ⅰ)设P(x,y),则Q(x,-1),F(0,1),由$\overrightarrow{QP}•\overrightarrow{QF}=\overrightarrow{FP}•\overrightarrow{FQ}$.根据向量数量积的坐标运算,即可求得动点P的轨迹C的方程;
(Ⅱ)法一:设$M({{x_0},\frac{x_0^2}{4}})$,利用点到直线的距离公式$d=\frac{{|{{x_0}-\frac{x_0^2}{4}-3}|}}{{\sqrt{2}}}=\frac{{{{({{x_0}-2})}^2}+8}}{{4\sqrt{2}}}$,由二次函数的性质可知:${x_0}=2时,{d_{min}}=\sqrt{2}$,求得M(2,1);
法二:当与直线y=x-3平行,且与曲线相切时的切点与与直线y=x-3的距离最短将直线方程代入抛物线方程,则△=0,即可求得m和x值,即可取得M到直线y=x-3的距离最短;
当与直线y=x-3平行,且与曲线相切时的切点与与直线y=x-3的距离最短.设切点为$M({{x_0},\frac{x_0^2}{4}})$,求导,求得切线斜率为$\frac{x_0}{2}=1$,即可求得,M点坐标,根据点到直线的距离公式即可求得,M到直线y=x-3的距离最短.
解答 解:(Ⅰ)设P(x,y),则Q(x,-1),F(0,1),
∴$\overrightarrow{QP}=({0,y+1}),\overrightarrow{QF}=({-x,2})$,$\overrightarrow{FP}=({x,y-1}),\overrightarrow{FQ}=({x,-2})$,…(4分)
$\overrightarrow{QP}•\overrightarrow{QF}=\overrightarrow{FP}•\overrightarrow{FQ}$.
∴2(y+1)=x2-2(y-1),化简得:x2=4y,
所求轨迹为:x2=4y…(6分)
(Ⅱ)法一:设$M({{x_0},\frac{x_0^2}{4}})$,则M到直线y=x-3的距离为$d=\frac{{|{{x_0}-\frac{x_0^2}{4}-3}|}}{{\sqrt{2}}}=\frac{{{{({{x_0}-2})}^2}+8}}{{4\sqrt{2}}}$,
∴${x_0}=2时,{d_{min}}=\sqrt{2}$,
此时M(2,1)为所求.…(12分)
法二:当与直线y=x-3平行,且与曲线相切时的切点与与直线y=x-3的距离最短.
设该直线方程为y=x+m,…(7分)
∴$\left\{\begin{array}{l}y=x+m\\{x^2}=4y\end{array}\right.⇒{x^2}-4x-4m=0,△=16+16m=0$,
解得:m=-1,x=2,
∴M(2,1)到直线y=x-3的距离最短,最短距离为$\sqrt{2}$.…(12分)
法三:当与直线y=x-3平行,且与曲线相切时的切点与与直线y=x-3的距离最短.
设切点为$M({{x_0},\frac{x_0^2}{4}})$,
轨迹方程可化为:$y=\frac{x^2}{4},y'=\frac{x}{2}$,切线斜率为$\frac{x_0}{2}=1$,
∴x0=2,
则M到直线y=x-3的距离为$d=\frac{{|{{x_0}-\frac{x_0^2}{4}-3}|}}{{\sqrt{2}}}=\frac{{{{({{x_0}-2})}^2}+8}}{{4\sqrt{2}}}$=$\sqrt{2}$,
则M到直线y=x-3的距离的最小值为$\sqrt{2}$,此时M(2,1).
点评 本题考查抛物线的轨迹方程,直线与抛物线的位置关系,考查点到直线距离公式的应用,导数的几何性质,考查计算能力,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
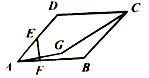 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )| A. | $\sqrt{7}-1$ | B. | 2 | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,6] | B. | [5,6] | C. | [25,36] | D. | [16,36] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com