
【题目】已知双曲线 ![]() =1(a>0,b>0),过其左焦点F作x轴的垂线,交双曲线于A,B两点,若双曲线的右顶点在以AB为直径的圆外,则双曲线离心率的取值范围是( )
=1(a>0,b>0),过其左焦点F作x轴的垂线,交双曲线于A,B两点,若双曲线的右顶点在以AB为直径的圆外,则双曲线离心率的取值范围是( )
A.(1, ![]() )
)
B.(1,2)
C.( ![]() ,+∞)
,+∞)
D.(2,+∞)
科目:高中数学 来源: 题型:
【题目】若关于![]() 的一元二次方程
的一元二次方程![]() 有实数根
有实数根![]() ,且
,且![]() ,则下列结论中错误的个数是( )
,则下列结论中错误的个数是( )
(1)当![]() 时,
时,![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ;(4)二次函数
;(4)二次函数![]() 的图象与
的图象与![]() 轴交点的坐标为(2,0)和(3,0)
轴交点的坐标为(2,0)和(3,0)
A. 1B. 2C. 3D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京、张家口2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量![]() 至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构通过对某企业今年的生产经营情况的调查,得到每月利润![]() (单位:万元)与相应月份数
(单位:万元)与相应月份数![]() 的部分数据如表:
的部分数据如表:
| 1 | 4 | 7 | 12 |
| 229 | 244 | 241 | 196 |
(1)根据如表数据,请从下列三个函数中选取一个恰当的函数描述![]() 与
与![]() 的变化关系,并说明理由,
的变化关系,并说明理由,![]() ,
,![]() ,
,![]() ;
;
(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数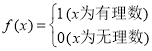 ,则关于函数
,则关于函数![]() 有如下说法:
有如下说法:
①![]() 的图像关于
的图像关于![]() 轴对称;
轴对称;
②方程![]() 的解只有
的解只有![]() ;
;
③任取一个不为零的有理数![]() ,
,![]() 对任意的
对任意的![]() 恒成立;
恒成立;
④不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.
为等边三角形.
其中正确的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com