
【题目】设不等式组 ![]() 表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离小于1的概率是( )
表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离小于1的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:到坐标原点的距离小于1的点,位于以原点O为圆心、半径为1的圆内,
区域D:设不等式组 ![]() 表示的平面区域为D,是表示正方形OABC,(如图)
表示的平面区域为D,是表示正方形OABC,(如图)
其中O为坐标原点,A(1,0),B(1,1),C(0,1).
因此在区域D内随机取一个点P,
则P点到坐标原点的距离大于1时,点P位于图中正方形OABC内,
且在扇形OAC的内部,如图中的扇形部分
∵S正方形OABC=12=1,S扇形= ![]() π12=
π12= ![]() ,所求概率为P=
,所求概率为P= ![]() =
= ![]() ,
,
故选:A.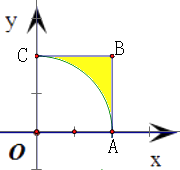
根据题意,在区域D内随机取一个点P,则P点到坐标原点的距离小于1时,点P位于图中正方形OABC内,且在扇形OAC的内部,如图中的扇形部分.因此算出图中扇形部分面积,再除以正方形OABC面积,即可求得本题的答案


科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有![]() 人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取
人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取![]() 人进行成绩抽样统计,先将
人进行成绩抽样统计,先将![]() 人按
人按![]() 进行编号.
进行编号.
(Ⅰ)如果从第![]() 行第
行第![]() 列的数开始向右读,请你依次写出最先检测的
列的数开始向右读,请你依次写出最先检测的![]() 个人的编号;(下面摘取了第
个人的编号;(下面摘取了第![]() 行 至第
行 至第![]() 行)
行)

(Ⅱ)抽的![]() 人的数学与地理的水平测试成绩如下表:
人的数学与地理的水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 |
| 4 |
| |
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() 人,若在该样本中,数学成绩优秀率为
人,若在该样本中,数学成绩优秀率为![]() ,求
,求![]() 的值.
的值.
(Ⅲ)将![]() 的
的![]() 表示成有序数对
表示成有序数对![]() ,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对
,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校对甲、乙两个班级进行了物理测验,成绩统计如下(每班50人):
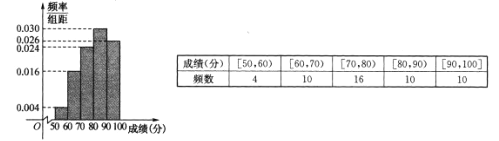
(1)估计甲班的平均成绩;
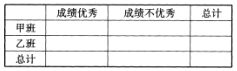
(2)成绩不低于80分记为“优秀”.请完成下面的![]() 列联表,并判断是否有85%的把握认为:“成绩优秀”与所在教学班级有关?
列联表,并判断是否有85%的把握认为:“成绩优秀”与所在教学班级有关?
(3)从两个班级,成绩在![]() 的学生中任选2人,记事件
的学生中任选2人,记事件![]() 为“选出的2人中恰有1人来自甲班”.求事件
为“选出的2人中恰有1人来自甲班”.求事件![]() 的概率
的概率![]() .
.
附: 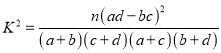
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料3千克;生产乙产品1桶需耗
原料3千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克,每桶甲产品的利润是300元,每桶乙产品的利润是400元,公司在要求每天消耗
原料1千克,每桶甲产品的利润是300元,每桶乙产品的利润是400元,公司在要求每天消耗![]() 原料都不超过12千克的条件下,生产产品
原料都不超过12千克的条件下,生产产品![]() 、产品
、产品![]() 的利润之和的最大值为( )
的利润之和的最大值为( )
A. 1800元 B. 2100元 C. 2400元 D. 2700元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取3个点,记落在直线![]() 右下方的点的个数为
右下方的点的个数为![]() ,求
,求![]() 的分布列以及期望.
的分布列以及期望.
参考公式: 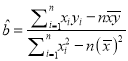 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点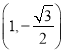 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是二次函数,若f(0)=0且f(x+1)﹣f(x)=x+1,求函数f(x)的解析式,并求出它在区间[﹣1,3]上的最大、最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com