
分析 (1)求出f'(x),由题意函数f(x)在x=1和x=-$\frac{2}{3}$处都取得极值.列出方程求解即可.
(2)原题等价于函数与y=f(x)与函数y=2c两个图象存在三个交点,求出f'(x)=3x2-x-2=(3x+2)(x-1),求出极值,列出不等式求解即可.
解答 (本小题满分13分)
解:(1)f'(x)=3x2+2ax+b…(1分)
由题意可知$\left\{\begin{array}{l}f'({-\frac{2}{3}})=0\\ f'(1)=0\end{array}\right.$,…(3分)
解得$\left\{\begin{array}{l}a=-\frac{1}{2}\\ b=-2\end{array}\right.$…(5分)
经检验,适合条件,所以$\left\{\begin{array}{l}a=-\frac{1}{2}\\ b=-2\end{array}\right.$…(6分)
(2)原题等价于函数与y=f(x)与函数y=2c两个图象存在三个交点,…(7分)
由(1)知f'(x)=3x2-x-2=(3x+2)(x-1),…(8分),
令(3x+2)(x-1)=0,可得x=-$\frac{2}{3}$,x=1;
x∈[-1,2],当x∈(-1,-$\frac{2}{3}$),x∈(1,2)时,f'(x)>0,函数是增函数,
x∈(-$\frac{2}{3}$,1)时,函数是减函数,
函数的极大值为:f(-$\frac{2}{3}$)=c+$\frac{22}{27}$,f(2)=2+c>c+$\frac{22}{27}$
极小值为:f(1)=-$\frac{3}{2}$+c,f(-1)=$\frac{1}{2}+c$>$-\frac{3}{2}+c$ …(11分)
∴x∈[-1,2]时,
可得$c+\frac{1}{2}≤2c<c+\frac{22}{27}$,∴$\frac{1}{2}≤c<\frac{22}{27}$…(13分)
点评 本题考查函数的导数的应用,函数的极值以及函数的端点函数值的关系,考查转化思想,难度比较大.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:解答题
设平面直角坐标系原点与极坐标极点重合,x轴正半轴与极轴重合,若已知曲线C的极坐标方程为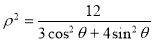 ,点F1、F2为其左、右焦点,直线l的参数方程为
,点F1、F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).
(t为参数,t∈R).
(Ⅰ)求曲线C的标准方程和直线l的普通方程;
(Ⅱ)若点P为曲线C上的动点,求点P到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | [2,+∞) | C. | (4,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
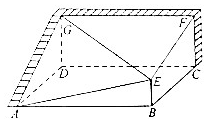 要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.
要利用现有的两面残墙,呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚(如图所示),所立柱子EB垂直于暖棚底面ABCD,其余四面计划用薄膜覆盖,已知底面ABCD是边长为2$\sqrt{6}$cm的正方形,且GD=2m,EB=1m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com