
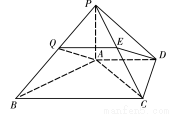
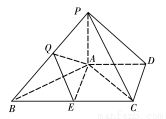
如图,在四棱锥P-ABCD中,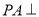 平面ABCD,AD//BC,BC=2AD,
平面ABCD,AD//BC,BC=2AD,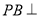 AC,Q是线段PB的中点.
AC,Q是线段PB的中点.
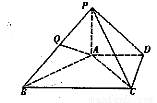
(1)求证: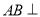 平面PAC;
平面PAC;
(2)求证:AQ//平面PCD.
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)要证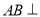 平面
平面 ,只要证:
,只要证: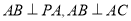 ,由题设
,由题设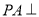 平面
平面
得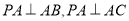 ,结合条件
,结合条件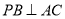 ,可证
,可证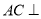 平面
平面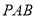 ,从而有
,从而有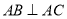 ,结论可证.
,结论可证.
(2)思路一: 取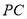 中点
中点 ,连接
,连接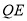 、
、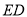 .因为
.因为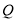 是线段
是线段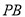 的中点,
的中点, 是
是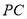 的中点,可证四边形
的中点,可证四边形 是平行四边形,从而有
是平行四边形,从而有 ∥
∥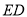 ,可证
,可证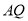 ∥平面
∥平面
思路二: 取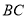 的中点
的中点 ,连接
,连接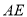 、
、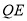 .因为
.因为 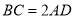 所以
所以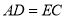 ,通过证明平面
,通过证明平面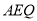 ∥平面
∥平面 ,达到证明
,达到证明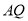 ∥平面
∥平面 的目的.
的目的.
证明:(1)因为 平面
平面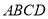 ,
,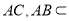 平面
平面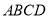
所以 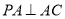 ,
,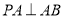 2分
2分
又因为 ,
,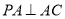 ,
,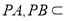 平面
平面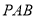 ,
, ,
,
所以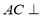 平面
平面 3分
3分
又因为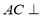 平面
平面 ,
,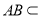 平面
平面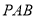 ,
,
所以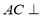
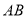 4分
4分
因为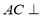
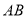 ,
,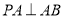 ,
,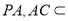 平面
平面 ,
,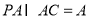 ,
,
所以  平面
平面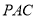 6分
6分
(2)方法一:取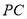 中点
中点 ,连接
,连接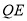 、
、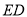 .因为
.因为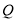 是线段
是线段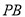 的中点,
的中点, 是
是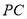 的中点,
的中点,
所以 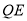 ∥
∥ ,
,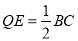 8分
8分
因为 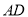 ∥
∥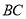 ,
,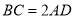
所以 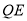 ∥
∥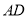 ,
,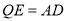
所以 四边形 是平行四边形, 9分
是平行四边形, 9分
所以  ∥
∥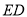 , 10分
, 10分
因为 ∥
∥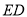 ,
,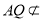 平面
平面 ,
,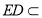 平面
平面
所以 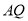 ∥平面
∥平面 . 12分
. 12分
方法二:取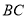 的中点
的中点 ,连接
,连接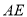 、
、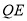 .因为
.因为 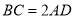 所以
所以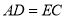
又 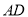 ∥
∥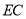 ,所以 四边形
,所以 四边形 是平行四边形,
是平行四边形,
所以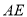 ∥
∥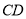
因为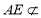 平面
平面 ,
,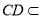 平面
平面 ,
,
所以 ∥平面
∥平面 8分
8分
因为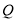 ,
, 分别是线段
分别是线段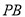 ,
,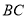 的中点,
的中点,
所以 ∥
∥ ,所以
,所以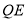 ∥平面
∥平面 10分
10分
因为 ,所以平面
,所以平面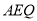 ∥平面
∥平面 11分
11分
因为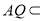 平面
平面 ,所以
,所以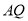 ∥平面
∥平面 . 12分
. 12分
考点:1、直线与平面垂直的判定与性质;2、直线与平面平行的判定与性质.


科目:高中数学 来源:2013-2014学年山东省烟台市高三5月适应性训练一文科数学试卷(解析版) 题型:解答题
某数学兴趣小组有男女生各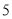 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为 .
.
(1)求 ,
, 的值;
的值;
(2)现从成绩高于 分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷(解析版) 题型:选择题
3名男生3名女生站成两排照相,要求每排3人且3名男生不在同一排,则不同的站法有
A.324种 B.360种 C.648种 D.684种
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试文科数学试卷(解析版) 题型:选择题
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是
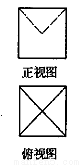
A.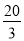 B.6 C.4 D.
B.6 C.4 D.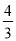
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省济南市高三3月考模拟考试理科数学试卷(解析版) 题型:选择题
已知中心在原点、焦点在x轴上的椭圆C1与双曲线C2有共同的焦点,设左右焦点分别为F1,F2,P是C1与C2在第一象限的交点, PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
PF1F2是以PF1为底边的等腰三角形,若椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )
(A)( ,+
,+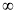 ) (B)(
) (B)(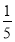 ,+
,+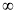 ) (C)(
) (C)( ,+
,+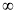 ) (D)(0,+
) (D)(0,+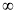 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com