
分析 依据椭圆的对称性,只要求出椭圆在第一角限内部分的面积即可,利用定积分的几何意义,即求出S=4${∫}_{0}^{a}$ydx=4${∫}_{0}^{a}$$\frac{b}{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx,由三角换元即得面积.
解答 解:因为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)关于x轴和y轴都是对称的,
所以所求之面积为S=4${∫}_{0}^{a}$ydx=4${∫}_{0}^{a}$$\frac{b}{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx,
令x=asinθ(0≤θ≤$\frac{π}{2}$),
则$\sqrt{{a}^{2}-{x}^{2}}$=$\sqrt{{a}^{2}-{a}^{2}si{n}^{2}θ}$=acosθ,
dx=acosθdθ,
∴S=4${∫}_{0}^{\frac{π}{2}}$$\frac{b}{a}$•acosθ•acosθdθ=4ab${∫}_{0}^{\frac{π}{2}}$(cosθ)2dθ
=4ab${∫}_{0}^{\frac{π}{2}}$$\frac{1+cos2θ}{2}$dθ=2ab[(θ+($\frac{1}{2}$sin2θ)]|${\;}_{0}^{\frac{π}{2}}$=πab.
故答案为:πab.
点评 本题考查运用定积分求面积,其关键是确定出被积函数和积分的上、下限.一般是应先根据题意,借助图形的直观性确定出被积函数,求出两条曲线的交点的坐标确定积分的上、下限,进而由定积分求出其面积.


科目:高中数学 来源: 题型:解答题
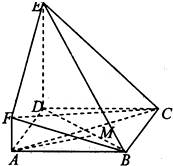 如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.
如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y+8=0 | B. | x+2y-8=0 | C. | x-2y-8=0 | D. | x-2y+8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 用平行于圆锥底面的平面截圆锥,截面和底面之间的部分是圆台 | |
| B. | 以直角梯形的一腰为旋转轴,另一腰为母线的旋转面是圆台的侧面 | |
| C. | 圆锥、圆柱、圆台的底面都是圆 | |
| D. | 圆台的母线延长后与轴交于同一点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
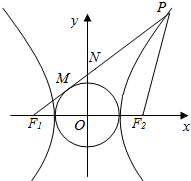 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P为双曲线右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则该双曲线的离心率e是$\frac{5}{3}$.
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P为双曲线右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则该双曲线的离心率e是$\frac{5}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com