
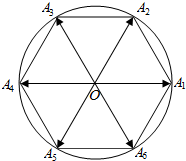
 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$. 分析 可假设该等差数列的前三项分别为θ1,θ2,θ3,然后画出图形,通过图形便可看出${θ}_{2}=\frac{π}{3}-{θ}_{1},{θ}_{2}=\frac{π}{3}+{θ}_{1}$,根据该数列为等差数列便可求出θ1,从而求出θ3,即得出该等差数列的第三项的值.
解答  解:设组成等差数列的前三项为:θ1,θ2,θ3,如图,$∠{A}_{1}OP={θ}_{1},{θ}_{1}<\frac{π}{6}$,则:
解:设组成等差数列的前三项为:θ1,θ2,θ3,如图,$∠{A}_{1}OP={θ}_{1},{θ}_{1}<\frac{π}{6}$,则:
${θ}_{2}=\frac{π}{3}-{θ}_{1},{θ}_{3}=\frac{π}{3}+{θ}_{1}$;
θ1,θ2,θ3成等差数列;
∴2θ2=θ1+θ3;
即$\frac{2π}{3}-2{θ}_{1}={θ}_{1}+\frac{π}{3}+{θ}_{1}$;
∴${θ}_{1}=\frac{π}{12}$;
${θ}_{3}=\frac{5π}{12}$;
即该等差数列的第三项为$\frac{5π}{12}$.
故答案为:$\frac{5π}{12}$.
点评 考查对圆内接正六边形的认识,数形结合解题的方法,等差数列的概念,及等差中项的概念.


科目:高中数学 来源: 题型:选择题
| A. | [1,10] | B. | $[{\sqrt{5},\sqrt{13}}]$ | C. | [1,5] | D. | $[{2,\sqrt{13}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.
如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
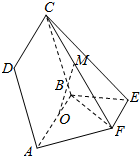 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)={x^2},g(x)=\sqrt{x^2}$ | B. | $f(x)=\frac{{{{(\sqrt{x})}^2}}}{x},g(x)=\frac{x}{{{{(\sqrt{x})}^2}}}$ | ||
| C. | f(x)=1,g(x)=(x-1)0 | D. | $f(x)=\frac{{{x^2}-9}}{x+3},g(x)=x-3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
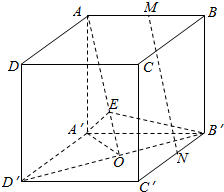 如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.
如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com