
 .
.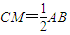 ;②
;②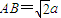 ;③CM⊥AB;④BC⊥AC.
;③CM⊥AB;④BC⊥AC.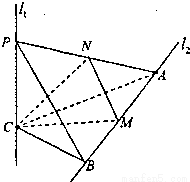
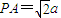 ,三边满足勾股定理则PC⊥AC,根据题意可知PC⊥AB,又AC∩AB=A,满足线面垂直的判定定理,从而得证;
,三边满足勾股定理则PC⊥AC,根据题意可知PC⊥AB,又AC∩AB=A,满足线面垂直的判定定理,从而得证;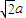 ,AC=a则BC=a,以C为坐标原点,
,AC=a则BC=a,以C为坐标原点,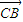 、
、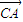 、
、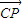 的方向为x、y、z轴正方向建立空间直角坐标系,
的方向为x、y、z轴正方向建立空间直角坐标系,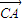 =(0,a,0)是平面PBC的一个法向量,然后求出平面MNC的法向量
=(0,a,0)是平面PBC的一个法向量,然后求出平面MNC的法向量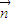 ,然后根据cos<
,然后根据cos<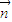 ,
,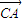 >=
>=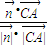 ,从而求出cosθ的值.
,从而求出cosθ的值.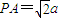 .
.
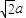 ,AC=a
,AC=a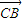 、
、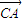 、
、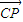 的方向为x、y、z轴正方向建立空间直角坐标系
的方向为x、y、z轴正方向建立空间直角坐标系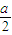 ,
,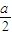 ,0),N(0,
,0),N(0,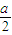 ,
,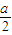 )
)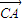 =(0,a,0)是平面PBC的一个法向量
=(0,a,0)是平面PBC的一个法向量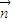 =(x,y,z)
=(x,y,z)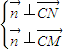 得
得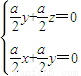
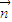 =(1,-1,1)为平面MNC的一个法向量
=(1,-1,1)为平面MNC的一个法向量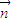 ,
,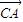 >=
>=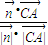 =
=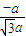 =-
=-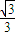
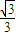


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
 如图,l1,l2是通过某市开发区中心0的两条南北和东西走向的道路,连接M、N两地的铁路是一段抛物线弧,它所在的抛物线关于直线L1对称.M到L1、L2的距离分别是2 km、4km,N到L1、L2的距离分别是3km、9km.
如图,l1,l2是通过某市开发区中心0的两条南北和东西走向的道路,连接M、N两地的铁路是一段抛物线弧,它所在的抛物线关于直线L1对称.M到L1、L2的距离分别是2 km、4km,N到L1、L2的距离分别是3km、9km.| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•福建模拟)如图,l1、l2是两条互相垂直的异面直线,点P、C在直线l1上,点A、B在直线l2上,M、N分别是线段AB、AP的中点,且PC=AC=a,PA=
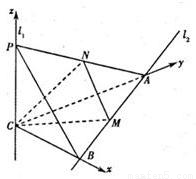
(2010•福建模拟)如图,l1、l2是两条互相垂直的异面直线,点P、C在直线l1上,点A、B在直线l2上,M、N分别是线段AB、AP的中点,且PC=AC=a,PA=| 2 |
| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:福建省模拟题 题型:解答题
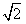 a,
a,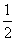 AB;②AB=
AB;②AB=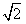 a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解.
a;③CM⊥AB;④BC⊥AC。请你从中再选择两个条件以确定cosθ的值,并求解. 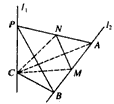
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com