曲线
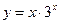
在点
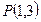
处的切线方程为
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
设函数
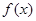
对
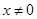
的任意实数,恒有
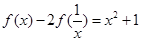
成立.
(I)求函数
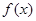
的解析式;
(II)用函数单调性的定义证明函数
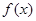
在
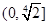
上是增函数
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)
已知函数
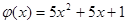
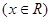
,函数
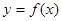
的图象与
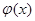
的图象关于点
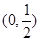
中心对称。
(1)求函数
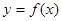
的解析式;
(2)如果
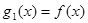
,
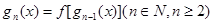
,试求出使
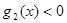
成立的
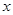
取值范围;
(3)是否存在区间
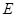
,使
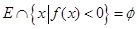
对于区间内的任意实数
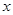
,只要
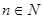
且
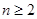
时,都有
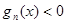
恒成立?
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(12分)已知函数
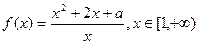
(1)当
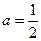
时,求函数
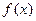
的最小值;
(2)若对任意的
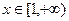
,
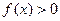
恒成立,试求实数
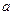
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)(第一问8分,第二问5分)
已知函数
f(
x)=2ln
x,
g(
x)=
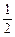 ax2
ax2+3
x.
(1)设直线
x=1与曲线
y=
f(
x)和
y=
g(
x)分别相交于点
P、
Q,且曲线
y=
f(
x)和
y=
g(
x)在点
P、
Q处的切线平行,若方程
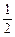 f
f(
x2+1)+
g(
x)=3
x+
k有四个不同的实根,求实数
k的取值范围;
(2)设函数
F(
x)满足
F(
x)+
x[
f′(
x)-
g′(
x)]=-3
x2-(
a+6)
x+1.其中
f′(
x),
g′(
x)分别是函数
f(
x)与
g(
x)的导函数;试问是否存在实数
a,使得当
x∈(0,1]时,
F(
x)取得最大值,若存在,求出
a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
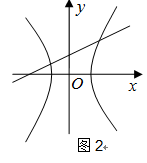
在平面直角坐标系
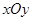
中,
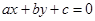
与
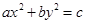
所表示的曲线如图2
所示,则常数
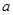
、
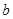
、
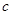
之间的关系可能是
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
用
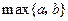
表示a,b两个数中的最大数,设
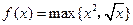
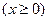
,那么由函数
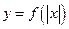
的图象、x轴、直线
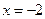
和直线
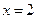
所围成的封闭图形的面积之和是
查看答案和解析>>

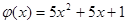
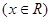 ,函数
,函数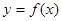 的图象与
的图象与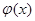 的图象关于点
的图象关于点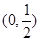 中心对称。
中心对称。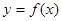 的解析式;
的解析式;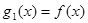 ,
,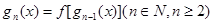 ,试求出使
,试求出使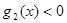 成立的
成立的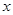 取值范围;
取值范围;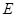 ,使
,使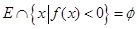 对于区间内的任意实数
对于区间内的任意实数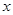 ,只要
,只要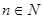 且
且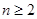 时,都有
时,都有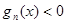 恒成立?
恒成立?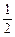 ax2+3x.
ax2+3x.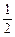 f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;