
【题目】设全集为R,函数 ![]() 的定义域为M,则RM为( )
的定义域为M,则RM为( )
A.[﹣1,1]
B.(﹣1,1)
C.(﹣∞,﹣1]∪[1,+∞)
D.(﹣∞,﹣1)∪(1,+∞)
【答案】D
【解析】解:由1﹣x2≥0,得﹣1≤x≤1,即M=[﹣1,1],又全集为R,
所以RM=(﹣∞,﹣1)∪(1,+∞).
故选D.
【考点精析】掌握集合的补集运算和函数的定义域及其求法是解答本题的根本,需要知道对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制;求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在![]() 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线![]() 上.
上.

(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线![]() 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量![]() ,并根据抽检数据绘制了如下图所示的频率分布直方图.
,并根据抽检数据绘制了如下图所示的频率分布直方图.
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)假设某企业每天由重金属污染造成的经济损失![]() (单位:元)与单位体积河水中重金属含量
(单位:元)与单位体积河水中重金属含量![]()
的关系式为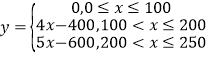 ,若将频率视为概率,在本年内随机抽取一天,试估计这天经济损失不超过500元的概率.
,若将频率视为概率,在本年内随机抽取一天,试估计这天经济损失不超过500元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为F1(﹣1,0)、F2(1,0),短轴的两个端点分别为B1 , B2
(1)若△F1B1B2为等边三角形,求椭圆C的方程;
(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了![]() 位育龄妇女,结果如表.
位育龄妇女,结果如表.
非一线 | 一线 | 总计 | |
愿生 |
|
|
|
不愿生 |
|
|
|
总计 |
|
|
|
附表:
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() 参照附表,得到的正确结论是( )
参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别有关”
的前提下,认为“生育意愿与城市级别有关”
B. 有![]() 以上的把握认为“生育意愿与城市级别有关”
以上的把握认为“生育意愿与城市级别有关”
C. 在犯错误的概率不超过![]() 的前提下,认为“生育意愿与城市级别无关”
的前提下,认为“生育意愿与城市级别无关”
D. 有![]() 以上的把握认为“生育意愿与城市级别无关”
以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季取暖时减少能源消耗,业主决定对房屋的屋顶和外墙喷涂某种新型隔热材料,该材料有效使用年限为20年.已知房屋外表喷一层这种隔热材料的费用为每毫米厚6万元,且每年的能源消耗费用![]() (万元)与隔热层厚度
(万元)与隔热层厚度![]() (毫米)满足关系:
(毫米)满足关系:![]() .设
.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)请解释![]() 的实际意义,并求
的实际意义,并求![]() 的表达式;
的表达式;
(2)当隔热层喷涂厚度为多少毫米时,业主所付的总费用![]() 最少?并求此时与不建隔热层相比较,业主可节省多少钱?
最少?并求此时与不建隔热层相比较,业主可节省多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com