
已知(x+1)n=a0+a1(x﹣1)+a2(x﹣1)+a3(x﹣1)3+…+an(x﹣1)n,(其中n∈N*)
(1)求a0及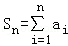 ;
;
(2)试比较Sn与(n﹣2)2n+2n2的大小,并说明理由.
(1)Sn=3n﹣2n
(2)当n=1时,3n>(n﹣1)2n+2n2;
当n=2,3时,3n<(n﹣1)2n+2n2;
当n≥4,n∈N*时,3n>(n﹣1)2n+2n2
解析试题分析:(1)令x=1,则a0=2n,令x=2,
则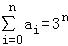 ,∴Sn=3n﹣2n; (3分)
,∴Sn=3n﹣2n; (3分)
(2)要比较Sn与(n﹣2)2n+2n2的大小,即比较:3n与(n﹣1)2n+2n2的大小,
当n=1时,3n>(n﹣1)2n+2n2;当n=2,3时,3n<(n﹣1)2n+2n2;
当n=4,5时,3n>(n﹣1)2n+2n2; (5分)
猜想:当n≥4时n≥4时,3n>(n﹣1)2n+2n2,下面用数学归纳法证明:
由上述过程可知,n=4n=4时结论成立,
假设当n=k(k≥4)n=k,(k≥4)时结论成立,即3n>(n﹣1)2n+2n2,
两边同乘以3 得:3k+1>3[(k﹣1)2k+2k2]=k2k+1+2(k+1)2+[(k﹣3)2k+4k2﹣4k﹣2]
而(k﹣3)2k+4k2﹣4k﹣2=(k﹣3)2k+4(k2﹣k﹣2)+6=(k﹣2)2k+4(k﹣2)(k+1)+6>0∴3k+1>[(k+1)﹣1]2k+1+2(k+1)2
即n=k+1时结论也成立,
∴当n≥4时,3n>(n﹣1)2n+2n2成立.
综上得,当n=1时,3n>(n﹣1)2n+2n2;
当n=2,3时,3n<(n﹣1)2n+2n2;当n≥4,n∈N*时,3n>(n﹣1)2n+2n2﹣﹣(10分)
考点:用数学归纳法证明不等式;数列的求和;二项式定理的应用
点评:本题是中档题,考查与n有关的命题,通过赋值法解答固定项,前n项和,以及数学归纳法的应用,考查逻辑推理能力,计算能力,常考题型


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com