
如图,三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,
![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;(Ⅱ)求二面角
;(Ⅱ)求二面角![]() 的大小.
的大小.
(Ⅰ)略(Ⅱ)![]()
方法(一)
(Ⅰ)由已知可得![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() . 1分由
. 1分由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() .又
.又![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() ,得
,得![]() .(也可以用三垂线定理直接证明
.(也可以用三垂线定理直接证明![]() )由中位线定理得,
)由中位线定理得,![]() ,于是
,于是![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .6分
.6分
(Ⅱ)由第(Ⅰ)问,已证明![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,则
,则![]() .已证明
.已证明![]() ,又
,又![]() ,则
,则![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() .由二面角的定义,得
.由二面角的定义,得![]() 为二面角
为二面角![]() 的平面角.…………9分
的平面角.…………9分
设![]() ,可求得
,可求得![]() ,
,![]() ,
,
在![]() 中,可求得
中,可求得![]() ,在
,在![]() 中,可求得
中,可求得![]() ,
,
在![]() 中,由余弦定理得,
中,由余弦定理得,![]() .
.
|
方法(二)
如图建立空间直角坐标系,设![]() ,
,
可求出以下各点的坐标:A(2,2,0),B(0,0,0),C(2,0,0),
P(0,0,2),E(1,0,1),F(1,1,1)
(Ⅰ)![]() ,
,![]() ,
,![]()
有![]() ,
,![]() ,
,
于是![]() ,
,![]() ,又
,又![]() ,
,
则![]() 平面
平面![]() .……6分
.……6分
(Ⅱ)![]() ,有
,有![]() ,
,![]() ,
,
于是![]() ,
,![]() ,由二面角定义,向量
,由二面角定义,向量![]() 与
与![]() 的夹角为所求.
的夹角为所求.
![]() ,所以
,所以![]() 为所求.……12分
为所求.……12分
本小题主要考查三棱锥,直线与平面的垂直,二面角的计算,考查空间想象能力、思维能力和运算能力.


科目:高中数学 来源: 题型:
如图:三棱锥![]() 中,
中,![]() ^底面
^底面![]() ,若底面
,若底面![]() 是边长为2的正三角形,且
是边长为2的正三角形,且![]() 与底面
与底面![]() 所成的角为
所成的角为![]() .若
.若![]() 是
是![]() 的中点,求:
的中点,求:
(1)三棱锥![]() 的体积;
的体积;
|

(2)异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源:2014届浙江省温州八校高三9月期初联考理科数学试卷(解析版) 题型:解答题
如图,三棱锥 中,
中, 底面
底面 ,
, ,
, ,
, 为
为 的中点,点
的中点,点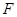 在
在 上,且
上,且 .
.

(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市青浦区高三上学期期终学习质量调研测试数学试卷 题型:解答题
(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分.
如图:三棱锥 中,
中, ^底面
^底面 ,若底面
,若底面 是边长为2的正三角形,且
是边长为2的正三角形,且
与底面 所成的角为
所成的角为 ,若
,若 是
是 的中点,
的中点,
求:(1)三棱锥 的体积;
的体积;
(2)异面直线 与
与 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com