Question

7．已知，在△ABC中，∠C=90°，BC=6，AC=8，点M、N在△ABC的边上，将△ABC沿直线MN对折后，它的一个顶点正好落在对边上，且折痕MN截△ABC所成的小三角形（即对折后的重叠部分）与△ABC相似．请在下列图（不一定都用，不够可添）中分别画出折痕MN各种可能的位置，并说明画法及直接写出折痕的长．

Answer 1

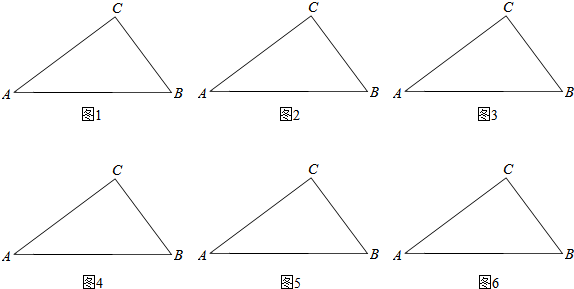
分析 由已知条件利用三角形中位线性质、直角三角形相似的性质及垂直平公线性质及三角形相似的判定定理，能求出结果．

解答 （本小题满分12分）
解：∵在△ABC中，∠C=90°，BC=6，AC=8，点M、N在△ABC的边上，将△ABC沿直线MN对折后，
它的一个顶点正好落在对边上，且折痕MN截△ABC所成的小三角形（即对折后的重叠部分）与△ABC相似，
∴前3图分别为△ABC的中位线，长度分别是3、4、5…（6分）


图4中N为AB的中点，MN垂直平分AB，MN=$\frac{15}{4}$，…（8分）
图5中D为AB的中点，MN垂直平分CD，MN=$\frac{125}{24}$．…（12分）

点评 本题考查使折痕MN截大三角形所成的小三角形（即对折后的重叠部分）与大三角相似的折痕位置的确定及折痕长度的求法，是中档题，解题时要认真审题，注意三角形相似的判定定理的合理运用．