
【题目】如图,DE是⊙O的直径,过⊙O上的点C作直线AB,交ED的延长线于点B,且OA=OB,CA=CB,连结EC,CD. 
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED= ![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
科目:高中数学 来源: 题型:
【题目】设0<a<1,已知函数f(x)= 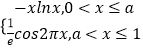 ,若对任意b∈(0,
,若对任意b∈(0, ![]() ),函数g(x)=f(x)﹣b至少有两个零点,则a的取值范围是( )
),函数g(x)=f(x)﹣b至少有两个零点,则a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)= ![]() +|lnx﹣a|,x∈[1,e2].
+|lnx﹣a|,x∈[1,e2].
(1)当a=3时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(2)若f(x)≤ ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且对任意正整数n都有an是n与Sn的等差中项,bn=an+1.
(1)求证:数列{bn}是等比数列,并求出其通项bn;
(2)若数列{Cn}满足Cn= ![]() 且数列{C
且数列{C ![]() }的前n项和为Tn , 证明Tn<2.
}的前n项和为Tn , 证明Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴与短轴之和为6,椭圆上任一点到两焦点
的长轴与短轴之和为6,椭圆上任一点到两焦点![]() ,
, ![]() 的距离之和为4.
的距离之和为4.
(1)求椭圆的标准方程;
(2)若直线![]() :
: ![]() 与椭圆交于
与椭圆交于![]() ,
, ![]() 两点,
两点, ![]() ,
, ![]() 在椭圆上,且
在椭圆上,且![]() ,
, ![]() 两点关于直线
两点关于直线![]() 对称,问:是否存在实数
对称,问:是否存在实数![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>1,函数f(x)=![]() ,g(x)=x+
,g(x)=x+![]() +4, 若
+4, 若![]() x1∈[1,3],
x1∈[1,3],![]() x2∈[0,3],使得f(x1)=g(x2)成立,则a的取值为__________.
x2∈[0,3],使得f(x1)=g(x2)成立,则a的取值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ ![]() ax2﹣2bx
ax2﹣2bx
(1)设点a=﹣3,b=1,求f(x)的最大值;
(2)当a=0,b=﹣ ![]() 时,方程2mf(x)=x2有唯一实数解,求正数m的取值范围.
时,方程2mf(x)=x2有唯一实数解,求正数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f′(x)﹣g(x)(f′(x)为函数f(x)的导函数)在[a,b]上有且只有两个不同的零点,则称f(x)是g(x)在[a,b]上的“关联函数”.若f(x)= ![]() +4x是g(x)=2x+m在[0,3]上的“关联函数”,则实数m的取值范围是( )
+4x是g(x)=2x+m在[0,3]上的“关联函数”,则实数m的取值范围是( )
A.![]()
B.[﹣1,0]
C.(﹣∞,﹣2]
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com