
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: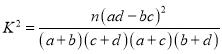
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(Ⅰ)详见解析;(Ⅱ)①![]() ;②数学期望为6,方差为2.4.
;②数学期望为6,方差为2.4.
【解析】
(1)完成列联表,由列联表,得![]() ,由此能在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关.
,由此能在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关.
(2)① 由题意所抽取的10名女市民中,经常网购的有![]() 人,偶尔或不用网购的有
人,偶尔或不用网购的有![]() 人,由此能选取的3人中至少有2人经常网购的概率.
人,由此能选取的3人中至少有2人经常网购的概率.
② 由![]() 列联表可知,抽到经常网购的市民的频率为:
列联表可知,抽到经常网购的市民的频率为:![]() ,由题意
,由题意![]() ,由此能求出随机变量
,由此能求出随机变量![]() 的数学期望
的数学期望![]() 和方差
和方差![]() .
.
解:(1)完成列联表(单位:人):
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 70 | 30 | 100 |
合计 | 120 | 80 | 200 |
由列联表,得:
![]() ,
,
∴能在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关.
(2)①由题意所抽取的10名女市民中,经常网购的有![]() 人,
人,
偶尔或不用网购的有![]() 人,
人,
∴选取的3人中至少有2人经常网购的概率为:
![]() .
.
② 由![]() 列联表可知,抽到经常网购的市民的频率为:
列联表可知,抽到经常网购的市民的频率为:![]() ,
,
将频率视为概率,
∴从我市市民中任意抽取一人,恰好抽到经常网购市民的概率为0.6,
由题意![]() ,
,
∴随机变量![]() 的数学期望
的数学期望![]() ,
,
方差D(X)=![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 与椭圆
与椭圆![]() 的离心率相同.
的离心率相同.

(1)求![]() 的值;
的值;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,交椭圆
,交椭圆![]() 于另一点
于另一点![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在
在![]() 之间).①求
之间).①求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点);②设
为坐标原点);②设![]() 的中点为
的中点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,试探究点
,试探究点![]() 是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (
(![]() 为常数,且
为常数,且![]() ).
).
(1)若当![]() 时,函数
时,函数![]() 与
与![]() 的图象有且只要一个交点,试确定自然数
的图象有且只要一个交点,试确定自然数![]() 的值,使得
的值,使得![]() (参考数值
(参考数值![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)当![]() 时,证明:
时,证明:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据统计,某蔬菜基地西红柿亩产量的增加量![]() (百千克)与某种液体肥料每亩使用量
(百千克)与某种液体肥料每亩使用量![]() (千克)之间的对应数据的散点图,如图所示.
(千克)之间的对应数据的散点图,如图所示.

(1)依据数据的散点图可以看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(若
并加以说明(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)求![]() 关于
关于![]() 的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量
的回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量![]() 约为多少?
约为多少?
附:相关系数公式
 ,参考数据:
,参考数据:![]() ,
,![]() .
.
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .
.
(1)直接写出函数![]() 的增区间(不需要证明);
的增区间(不需要证明);
(2)求出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com