
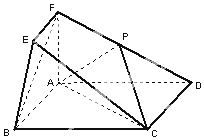
 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=l,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=l,点P在棱DF上.分析 (Ⅰ)连接BD,交AC于点O,连接OP,由P是DF中点,O为矩形ABCD 对角线的交点,利用三角形中位线定理可得BF∥OP,再由线面平行的判定可得BF∥平面ACP.
(II)由已知可证平面CDFE⊥平面ADF,在Rt△DAF中,求得A到平面CDFE的高h,再求出三角形PEC的面积,利用等积法求得三棱锥P-BEC的体积.
解答 (Ⅰ)证明:连接BD,交AC于点O,连接OP.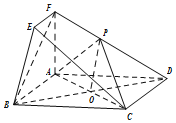
∵P是DF中点,O为矩形ABCD 对角线的交点,
∴OP为三角形BDF中位线,
∴BF∥OP,
∵BF?平面ACP,OP?平面ACP,
∴BF∥平面ACP.
(II)解:∵∠BAF=90°,∴AB⊥AF,
又四边形ABCD为矩形,∴AB⊥AD,
∴AB⊥平面ADF,又AB∥EF,EF?平面CDFE,
∴平面CDFE⊥平面ADF,
在Rt△DAF中,由AD=2,AF=l,求得A到平面CDFE的高h=$\frac{2}{\sqrt{5}}$,
又${S}_{△PEC}=\frac{1}{2}{S}_{四边形CDFE}=\frac{1}{2}×\frac{1}{2}(\frac{1}{2}+1)×\sqrt{5}$=$\frac{3\sqrt{5}}{8}$.
∴${V_{P-BEC}}={V_{B-PEC}}=\frac{1}{3}{S_{△PEC}}h=\frac{1}{3}×\frac{{3\sqrt{5}}}{8}×\frac{2}{{\sqrt{5}}}=\frac{1}{4}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=84x | B. | y=21(1+4x) | C. | y=21x4 | D. | y=21(1+x)4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
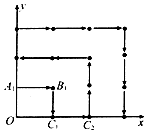 某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )| A. | 1936 | B. | 2016 | C. | 2017 | D. | 2208 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2tanα | B. | 2tanα | C. | $\frac{-2}{tanα}$ | D. | $\frac{2}{tanα}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com