Question

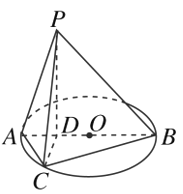
【题目】如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，M是PD的中点．

（1）求证：OM∥平面PAB；

（2）求证：平面PBD⊥平面PAC．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；

【解析】

（1）易知OM是△PBD的中位线，可知OM∥PB，进而可证明OM∥平面PAB；（2）底面ABCD是菱形，可知BD⊥AC，再由PA⊥平面ABCD，可得BD⊥PA，进而可证明BD⊥平面PAC，即可证明平面PBD⊥平面PAC．

证明：（1）∵在△PBD中，O、M分别是BD、PD的中点，

∴OM是△PBD的中位线，∴OM∥PB，

∵OM平面PAB，PB平面PAB，

∴OM∥平面PAB；

（2）∵底面ABCD是菱形，∴BD⊥AC，

∵PA⊥平面ABCD，BD平面ABCD，∴BD⊥PA．

∵AC平面PAC，PA平面PAC，AC∩PA=A，∴BD⊥平面PAC，

∵BD平面PBD，

∴平面PBD⊥平面PAC．