
分析 (Ⅰ)求出圆心与半径,即可求圆C的方程;
(Ⅱ)分类讨论,利用圆心到直线的距离等于半径,即可求过点M(3,1)的圆C的切线方程.
解答 解:(Ⅰ)由题意,得圆心C的坐标为(1,2),---------(2分)
直径$2r=\sqrt{16+0}=4$.故半径r=2----------(4分)
所以,圆C的方程为(x-1)2+(y-2)2=4.--------(5分)
(Ⅱ)∵(3-1)2+(1-2)2=5>4,∴点M在圆C外部.
(1)当过点M的直线斜率不存在时,直线方程为x=3,
即x-3=0.------------------------------------------------------------(7分)
又点C(1,2)到直线x-3=0的距离d=3-1=2=r,
即此时满足题意,所以直线x=3是圆的切线.
(2)当切线的斜率存在时,设切线方程为y-1=k(x-3),
即kx-y+1-3k=0,-------------------------------(8分)
则圆心C到切线的距离d=$\frac{|k-2+1-3k|}{\sqrt{k2+1}}$=r=2,------(10分)(距离公式1分)
解得k=$\frac{3}{4}$.-------------------------------------(11分)
∴切线方程为y-1=$\frac{3}{4}$(x-3),即3x-4y-5=0.
综上可得,过点M的圆C的切线方程为x-3=0或3x-4y-5=0.-------(12分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查分类讨论的数学思想,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥D-ABCO的底面是直角梯形,已知OC∥AB,AB⊥BC,OA=OB,OD⊥DA,AB=2OC,OC=OD=BC=DA=1,DB=$\sqrt{3}$.
如图,四棱锥D-ABCO的底面是直角梯形,已知OC∥AB,AB⊥BC,OA=OB,OD⊥DA,AB=2OC,OC=OD=BC=DA=1,DB=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{4}$或-$\frac{1}{4}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
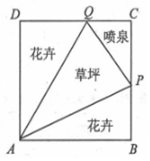 如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.
如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
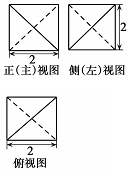
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com