
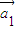 •
•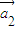 ,…
,… 存在n个不全为零的实数k1,k2,…,kn,使得k1
存在n个不全为零的实数k1,k2,…,kn,使得k1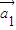 +k2
+k2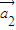 +…,kn
+…,kn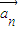 =成立,则称向量
=成立,则称向量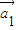 、
、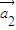 ,…
,…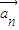 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明 =(1,2),
=(1,2),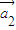 =(1,-1),
=(1,-1),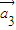 =(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).
=(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况). 科目:高中数学 来源:2014届海南省高一第一学期期终考试数学试卷 题型:填空题
若对n个向量 ,存在n个不全为零的实数k1,k2,…,kn,使得
,存在n个不全为零的实数k1,k2,…,kn,使得 =
= 成立,则称向量
成立,则称向量 为“线性相关”.依此规定,若
为“线性相关”.依此规定,若  =(1,0),
=(1,0),  =(1,-1),
=(1,-1),  =(2,2) “线性相关”,则
=(2,2) “线性相关”,则 的比值是
的比值是
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省清远市连州中学高三(上)10月月考数学试卷(理科)(解析版) 题型:填空题
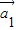 •
•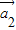 ,…
,…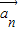 存在n个不全为零的实数k1,k2,…,kn,使得k1
存在n个不全为零的实数k1,k2,…,kn,使得k1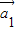 +k2
+k2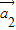 +…,kn
+…,kn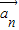 =成立,则称向量
=成立,则称向量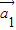 、
、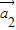 ,…
,…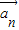 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明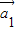 =(1,2),
=(1,2),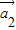 =(1,-1),
=(1,-1),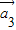 =(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).
=(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).查看答案和解析>>
科目:高中数学 来源:2010年贵州省黔南州都匀市高考数学模拟试卷(一)(解析版) 题型:解答题
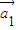 •
•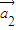 ,…
,…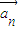 存在n个不全为零的实数k1,k2,…,kn,使得k1
存在n个不全为零的实数k1,k2,…,kn,使得k1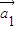 +k2
+k2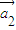 +…,kn
+…,kn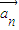 =成立,则称向量
=成立,则称向量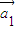 、
、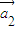 ,…
,…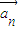 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明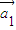 =(1,2),
=(1,2), =(1,-1),
=(1,-1),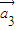 =(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).
=(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).查看答案和解析>>
科目:高中数学 来源:2010年新教材高考数学模拟题详解精编试卷(6)(解析版) 题型:解答题
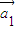 •
•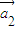 ,…
,…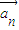 存在n个不全为零的实数k1,k2,…,kn,使得k1
存在n个不全为零的实数k1,k2,…,kn,使得k1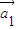 +k2
+k2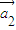 +…,kn
+…,kn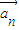 =成立,则称向量
=成立,则称向量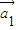 、
、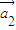 ,…
,…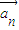 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明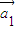 =(1,2),
=(1,2),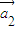 =(1,-1),
=(1,-1),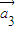 =(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).
=(2,2)“线性相关”的实数k1,k2,k3依次可以取 (写出一组数值即中,不必考虑所有情况).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com