
【题目】盒子中装有四张大小形状均相同的卡片,卡片上分别标有数![]() 其中
其中![]() 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件![]() “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率![]() 与事件
与事件![]() “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率![]() ;
;
(2)在两次试验中,记两次得到的数分别为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]()
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() .
.
(1)求以右焦点为圆心,与双曲线![]() 的渐近线相切的圆的方程;
的渐近线相切的圆的方程;
(2)若经过点![]() 的直线与双曲线
的直线与双曲线![]() 的右支交于不同两点
的右支交于不同两点![]() 、
、![]() ,求线段
,求线段![]() 的中垂线
的中垂线![]() 在
在![]() 轴上截距
轴上截距![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学研究证实,二氧化碳等温空气体的排放(简称碳排放)对全球气候和生态环境产生了负面影响,环境部门对![]() 市每年的碳排放总量规定不能超过
市每年的碳排放总量规定不能超过![]() 万吨,否则将采取紧急限排措施.已知
万吨,否则将采取紧急限排措施.已知![]() 市
市![]() 年的碳排放总量为
年的碳排放总量为![]() 万吨,通过技术改造和倡导低碳生活等措施,此后每年的碳排放量比上一年的碳排放总量减少
万吨,通过技术改造和倡导低碳生活等措施,此后每年的碳排放量比上一年的碳排放总量减少![]() .同时,因经济发展和人口增加等因素,每年又新增加碳排放量
.同时,因经济发展和人口增加等因素,每年又新增加碳排放量![]() 万吨
万吨![]() .
.
(1)求![]() 市
市![]() 年的碳排放总量(用含
年的碳排放总量(用含![]() 的式子表示);
的式子表示);
(2)若![]() 市永远不需要采取紧急限排措施,求
市永远不需要采取紧急限排措施,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为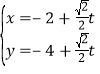 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记直线
,记直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)求曲线![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)证明:![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2![]() +sinB·cos2
+sinB·cos2![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S=![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为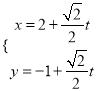 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com