
【题目】已知函数![]() .
.
(Ⅰ)当a>0时,求函数f(x)的单调递减区间;
(Ⅱ)当a=0时,设函数g(x)=xf(x)﹣k(x+2)+2.若函数g(x)在区间![]() 上有两个零点,求实数k的取值范围.
上有两个零点,求实数k的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先求函数导数,根据导函数零点讨论导函数符号,进而确定单调减区间(2)先利用分参法将方程零点转化为研究函数![]() 值域,利用导数研究函数
值域,利用导数研究函数![]() 单调性,最后根据单调性确定函数值域
单调性,最后根据单调性确定函数值域
试题解析:解:(Ⅰ)f(x)的定义域为(0,+∞),
f(x)的导数为f′(x)=﹣ax+1+a﹣![]() =﹣
=﹣![]() (a>0),
(a>0),
①当a∈(0,1)时,![]() .
.
由f'(x)<0,得![]() 或x<1.
或x<1.
当x∈(0,1),![]() 时,f(x)单调递减.
时,f(x)单调递减.
∴f(x)的单调递减区间为(0,1),![]() ;
;
②当a=1时,恒有f'(x)≤0,∴f(x)单调递减.
∴f(x)的单调递减区间为(0,+∞);
③当a∈(1,+∞)时,![]() .
.
由f'(x)<0,得x>1或![]() .
.
∴当![]() ,x∈(1,+∞)时,f(x)单调递减.
,x∈(1,+∞)时,f(x)单调递减.
∴f(x)的单调递减区间为![]() ,(1,+∞).
,(1,+∞).
综上,当a∈(0,1)时,f(x)的单调递减区间为(0,1),![]() ;
;
当a=1时,f(x)的单调递减区间为(0,+∞);
当a∈(1,+∞)时,f(x)的单调递减区间为![]() ,(1,+∞).
,(1,+∞).
(Ⅱ)g(x)=x2﹣xlnx﹣k(x+2)+2在![]() 上有零点,
上有零点,
即关于x的方程![]() 在
在![]() 上有两个不相等的实数根.
上有两个不相等的实数根.
令函数![]() .
.
则![]() .
.
令函数![]() .
.
则![]() 在
在![]() 上有p'(x)≥0.
上有p'(x)≥0.
故p(x)在![]() 上单调递增.
上单调递增.
∵p(1)=0,∴当![]() 时,有p(x)<0即h'(x)<0.∴h(x)单调递减;
时,有p(x)<0即h'(x)<0.∴h(x)单调递减;
当x∈(1,+∞)时,有p(x)>0即h'(x)>0,∴h(x)单调递增.
∵![]() ,h(1)=1,
,h(1)=1,![]()
![]() ,
,
∴k的取值范围为![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,a2=2,an+2=(1+cos2 ![]() )an+sin2
)an+sin2 ![]() ,则该数列的前12项和为( )
,则该数列的前12项和为( )
A.211
B.212
C.126
D.147
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数y=f(x)的图象过点 ![]() .
.
(1)求函数f(x)的解析式
(2)记g(x)=f(x)+x , 判断g(x)在(1,+∞)上的单调性,并证明之.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下:
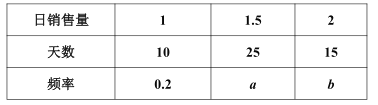
若以上表中频率作为概率,且每天的销售量相互独立.
(1)求5天中该种商品恰好有两天的日销售量为1.5吨的概率;
(2)已知每吨该商品的销售利润为2千元, ![]() 表示该种商品某两天销售利润的和(单位:千元),求
表示该种商品某两天销售利润的和(单位:千元),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+b满足f(1)=0,且在x=2时函数取得极值.
(1)求a,b的值;
(2)求函数f(x)的单调区间;
(3)求函数f(x)在区间[0,t](t>0)上的最大值g(t)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 是
是![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于
于![]() 点.
点.

(1)证明:抛物线![]() 在
在![]() 点处的切线与
点处的切线与![]() 平行;
平行;
(2)是否存在实数![]() ,使以
,使以![]() 为直径的圆
为直径的圆![]() 经过
经过![]() 点?若存在,求出
点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=ax3﹣x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA , 0)(xA>0); 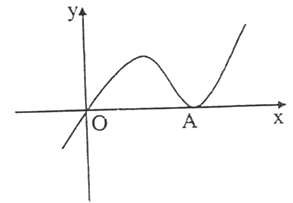
(1)用反证法证明常数c≠0;
(2)如果 ![]() ,求函数的解析式.
,求函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com