
【题目】已知在函数![]() (
(![]() )的所有切线中,有且仅有一条切线
)的所有切线中,有且仅有一条切线![]() 与直线
与直线![]() 垂直.
垂直.
(1)求![]() 的值和切线
的值和切线![]() 的方程;
的方程;
(2)设曲线![]() 在任一点处的切线倾斜角为
在任一点处的切线倾斜角为![]() ,求
,求![]() 的取值范围.
的取值范围.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数fk(x)=xk+bx+c(k∈N* , b,c∈R),g(x)=logax(a>0,a≠1).
(1)若b+c=1,且fk(1)=g( ![]() ),求a的值;
),求a的值;
(2)若k=2,记函数fk(x)在[﹣1,1]上的最大值为M,最小值为m,求M﹣m≤4时的b的取值范围;
(3)判断是否存在大于1的实数a,使得对任意x1∈[a,2a],都有x2∈[a,a2]满足等式:g(x1)+g(x2)=p,且满足该等式的常数p的取值唯一?若存在,求出所有符合条件的a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆与双曲线有相同的焦点![]() ,
,![]() ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为![]() ,直线
,直线![]() 与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为
与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
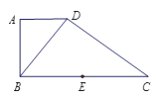
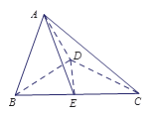
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() , 得到如
, 得到如
图所示的空间几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图). 
(1)分别写出两种产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从![]() 个招标问题中随机抽取
个招标问题中随机抽取![]() 个问题,已知这
个问题,已知这![]() 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的![]() 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为![]() ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对![]() 道题目的概率;
道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :
: ![]() ,命题
,命题![]()
![]() .
.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(3)若命题“![]() ”为真命题,且命题“
”为真命题,且命题“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com