
ЁОЬтФПЁПФГаЃдкИпвЛФъМЖвЛАржССљАрНјааСЫЁАЩчЭХЛюЖЏЁБТњвтЖШЕїВщЃЈНсЙћжЛгаЁАТњвтЁБКЭЁАВЛТњвтЁБСНжжЃЉЃЌДгБЛЕїВщЕФбЇЩњжаЫцЛњГщШЁСЫ50ШЫЃЌОпЬхЕФЕїВщНсЙћШчБэЃК
АрКХ | вЛАр | ЖўАр | Ш§Ар | ЫФАр | ЮхАр | СљАр |
ЦЕЪ§ | 4 | 5 | 11 | 8 | 10 | 12 |
ТњвтШЫЪ§ | 3 | 2 | 8 | 5 | 6 | 6 |
ЯжДгвЛАрКЭЖўАрЕїВщЖдЯѓжаЫцЛњбЁШЁ4ШЫНјаазЗзйЕїВщЃЌдђбЁжаЕФ4ШЫжаЧЁга2ШЫВЛТњвтЕФИХТЪЮЊ___________ЃЛШєНЋвдЩЯЭГМЦЪ§ОнжабЇЩњГжТњвтЬЌЖШЕФЦЕТЪЪгЮЊИХТЪЃЌдкИпвЛФъМЖШЋЬхбЇЩњжаЫцЛњГщШЁ3УћбЇЩњЃЌМЧЦфжаТњвтЕФШЫЪ§ЮЊXЃЌдђЫцЛњБфСПXЕФЪ§бЇЦкЭћЪЧ___________
ЁОД№АИЁП![]()
![]() ЃЛ
ЃЛ
ЁОНтЮіЁП
ЕквЛПеЃКРћгУЙХЕфИХаЭЕФИХТЪЙЋЪНМЦЫуМДПЩЃЛ
ЕкЖўПеЃКXЕФЫљгаПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЌЧѓГіЗжВМСаЃЌНјЖјЭЈЙ§Ъ§бЇЦкЭћМЦЫуЙЋЪНМДПЩЕУГі.
НтЃКЕквЛПеЃКДгвЛАрКЭЖўАрЕїВщЖдЯѓжаЫцЛњбЁШЁ4ШЫНјаазЗзйЕїВщЃЌдђбЁжаЕФ4ШЫжаЧЁга2ШЫВЛТњвтЕФИХТЪЮЊ![]() ЃЛ
ЃЛ
ЕкЖўПеЃКдкИпвЛФъМЖШЋЬхбЇЩњжаЫцЛњГщШЁ1УћбЇЩњЃЌ
ЦфТњвтИХТЪЮЊ![]() ЃЌ
ЃЌ
XЕФЫљгаПЩФмШЁжЕЮЊ0ЃЌ1ЃЌ2ЃЌ3ЃЎ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЗжВМСаШчЯТЃК
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() жИЪ§ЪЧгУЬхжиЙЋНяЪ§Г§вдЩэИпУзЪ§ЕФЦНЗНЕУГіЕФЪ§зжЃЌЪЧЙњМЪЩЯГЃгУЕФКтСПШЫЬхХжЪнГЬЖШвдМАЪЧЗёНЁПЕЕФвЛИіБъзМЃЎЖдгкИпжаФаЬхг§ЬиГЄЩњЖјбдЃЌЕБ
жИЪ§ЪЧгУЬхжиЙЋНяЪ§Г§вдЩэИпУзЪ§ЕФЦНЗНЕУГіЕФЪ§зжЃЌЪЧЙњМЪЩЯГЃгУЕФКтСПШЫЬхХжЪнГЬЖШвдМАЪЧЗёНЁПЕЕФвЛИіБъзМЃЎЖдгкИпжаФаЬхг§ЬиГЄЩњЖјбдЃЌЕБ![]() Ъ§жЕДѓгкЛђЕШгк20.5ЪБЃЌЮвУЧЫЕЬхжиНЯжиЃЌЕБ
Ъ§жЕДѓгкЛђЕШгк20.5ЪБЃЌЮвУЧЫЕЬхжиНЯжиЃЌЕБ![]() Ъ§жЕаЁгк20.5ЪБЃЌЮвУЧЫЕЬхжиНЯЧсЃЌЩэИпДѓгкЛђЕШгк
Ъ§жЕаЁгк20.5ЪБЃЌЮвУЧЫЕЬхжиНЯЧсЃЌЩэИпДѓгкЛђЕШгк![]() ЮвУЧЫЕЩэИпНЯИпЃЌЩэИпаЁгк170cmЮвУЧЫЕЩэИпНЯАЋЃЎ
ЮвУЧЫЕЩэИпНЯИпЃЌЩэИпаЁгк170cmЮвУЧЫЕЩэИпНЯАЋЃЎ
ЃЈЂёЃЉвбжЊФГИпжаЙВга32УћФаЬхг§ЬиГЄЩњЃЌЦфЩэИпгы![]() жИЪ§ЕФЪ§ОнШчЩЂЕуЭМЃЌЧыИљОнЫљЕУаХЯЂЃЌЭъГЩЯТЪіСаСЊБэЃЌВЂХаЖЯЪЧЗёга
жИЪ§ЕФЪ§ОнШчЩЂЕуЭМЃЌЧыИљОнЫљЕУаХЯЂЃЌЭъГЩЯТЪіСаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊФаЩњЕФЩэИпЖд
ЕФАбЮеШЯЮЊФаЩњЕФЩэИпЖд![]() жИЪ§гагАЯьЃЎ
жИЪ§гагАЯьЃЎ

ЩэИпНЯАЋ | ЩэИпНЯИп | КЯМЦ | |
ЬхжиНЯЧс | |||
ЬхжиНЯжи | |||
КЯМЦ |
ЃЈЂђЃЉЂйДгЩЯЪі32УћФаЬхг§ЬиГЄЩњжаЫцЛњбЁШЁ8УћЃЌЦфЩэИпКЭЬхжиЕФЪ§ОнШчБэЫљЪОЃК
БрКХ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ЩэИп | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
Ьхжи | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
ИљОнзюаЁЖўГЫЗЈЕФЫМЯыгыЙЋЪНЧѓЕУЯпадЛиЙщЗНГЬЮЊ![]() ЃЎРћгУвбОЧѓЕУЕФЯпадЛиЙщЗНГЬЃЌЧыЭъЩЦЯТСаВаВюБэЃЌВЂЧѓ
ЃЎРћгУвбОЧѓЕУЕФЯпадЛиЙщЗНГЬЃЌЧыЭъЩЦЯТСаВаВюБэЃЌВЂЧѓ![]() ЃЈНтЪЭБфСПЃЈЩэИпЃЉЖдгкдЄБЈБфСПЃЈЬхжиЃЉБфЛЏЕФЙБЯзжЕЃЉЃЈБЃСєСНЮЛгааЇЪ§зжЃЉЃЛ
ЃЈНтЪЭБфСПЃЈЩэИпЃЉЖдгкдЄБЈБфСПЃЈЬхжиЃЉБфЛЏЕФЙБЯзжЕЃЉЃЈБЃСєСНЮЛгааЇЪ§зжЃЉЃЛ
БрКХ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ЬхжиЃЈkgЃЉ | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
ВаВю |
|
|
|
|
|
|
|
ЂкЭЈЙ§ВаВюЗжЮіЃЌЖдгкВаВюЕФзюДѓЃЈОјЖджЕЃЉЕФФЧзщЪ§ОнЃЌашвЊШЗШЯдкбљБОЕуЕФВЩМЏжаЪЧЗёгаШЫЮЊЕФДэЮѓЃЌвбжЊЭЈЙ§жиаТВЩМЏЗЂЯжЃЌИУзщЪ§ОнЕФЬхжигІИУЮЊ![]() ЃЎаЁУїжиаТИљОнзюаЁЖўГЫЗЈЕФЫМЯыгыЙЋЪНЃЌвбЫуГі
ЃЎаЁУїжиаТИљОнзюаЁЖўГЫЗЈЕФЫМЯыгыЙЋЪНЃЌвбЫуГі![]() ЃЌЧыдкаЁУїЫљЫуЕФЛљДЁЩЯЧѓГіФаЬхг§ЬиГЄЩњЕФЩэИпгыЬхжиЕФЯпадЛиЙщЗНГЬЃЎ
ЃЌЧыдкаЁУїЫљЫуЕФЛљДЁЩЯЧѓГіФаЬхг§ЬиГЄЩњЕФЩэИпгыЬхжиЕФЯпадЛиЙщЗНГЬЃЎ
ВЮПМЪ§ОнЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ВЮПМЙЋЪНЃК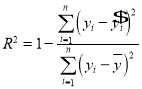 ЃЌ
ЃЌ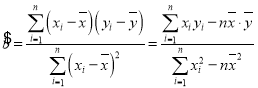 ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБЫФРтжљABCDЉA1B1C1D1жаЃЌЕзУцABCDЮЊСтаЮЃЌЁЯABCЃН60ЁуЃЌAA1![]() ABЃЌMЃЌNЗжБ№ЮЊABЃЌAA1ЕФжаЕу.
ABЃЌMЃЌNЗжБ№ЮЊABЃЌAA1ЕФжаЕу.
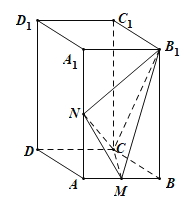
ЃЈ1ЃЉЧѓжЄЃКЦНУцB1NCЁЭЦНУцCMNЃЛ
ЃЈ2ЃЉШєABЃН2ЃЌЧѓЕуNЕНЦНУцB1MCЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉШє![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШєЗНГЬ![]() дкЧјМф
дкЧјМф![]() ФкгаНтЃЌЧѓЪЕЪ§
ФкгаНтЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ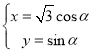 (
(![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌвд
ЮЊМЋЕуЃЌвд![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]()
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭжБЯп
ЕФЦеЭЈЗНГЬКЭжБЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉвбжЊЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊЧњЯп
ЮЊЧњЯп![]() ЩЯЕФЖЏЕуЃЌЧѓЯпЖЮ
ЩЯЕФЖЏЕуЃЌЧѓЯпЖЮ![]() ЕФжаЕу
ЕФжаЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЕФзюДѓжЕ.ВЂЧѓДЫЪБЕу
ЕФОрРыЕФзюДѓжЕ.ВЂЧѓДЫЪБЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉЕБ![]() ЃЌЩшКЏЪ§
ЃЌЩшКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЧЁгавЛИіСуЕуЃЌЧѓе§Ъ§aЕФШЁжЕЗЖЮЇЃЛ
ЩЯЧЁгавЛИіСуЕуЃЌЧѓе§Ъ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌжЄУїЃКЖдгк
ЪБЃЌжЄУїЃКЖдгк![]() ЃЌга
ЃЌга .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() ЃЌЧвИУЭждВЕФЖЬжсЖЫЕугыСННЙЕу
ЃЌЧвИУЭждВЕФЖЬжсЖЫЕугыСННЙЕу![]() ЃЌ
ЃЌ![]() ЕФеХНЧЮЊжБНЧ.
ЕФеХНЧЮЊжБНЧ.
ЃЈ1ЃЉЧѓЭждВEЕФЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЧваБТЪДѓгк0ЕФжБЯп
ЧваБТЪДѓгк0ЕФжБЯп![]() гыЭждВEЯрНЛгкЕуPЃЌQЃЌжБЯпAPЃЌAQгыyжсЯрНЛгкMЃЌNСНЕуЃЌЧѓ
гыЭждВEЯрНЛгкЕуPЃЌQЃЌжБЯпAPЃЌAQгыyжсЯрНЛгкMЃЌNСНЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓжБЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈЂђЃЉЩш![]() ЮЊЧњЯп
ЮЊЧњЯп![]() ЩЯЕФЕуЃЌ
ЩЯЕФЕуЃЌ![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌШє
ЃЌШє![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЪЧВшЕФЙЪЯчЃЌвВЪЧВшЮФЛЏЕФЗЂдДЕи.жаЙњВшЕФЗЂЯжКЭРћгУвбгаЫФЧЇЦпАйЖрФъЕФРњЪЗЃЌЧвГЄЪЂВЛЫЅЃЌДЋБщШЋЧђ.ЮЊСЫКыбяжаЙњВшЮФЛЏЃЌФГОЦЕъЭЦГіЬиЩЋВшЪГЦЗЁАН№нцХХЙЧВшЁБЃЌЮЊСЫНтУПКјЁАН№нцХХЙЧВшЁБжаЫљЗХВшвЖСП![]() ПЫгыЪГПЭЕФТњвтТЪ
ПЫгыЪГПЭЕФТњвтТЪ![]() ЕФЙиЯЕЃЌЭЈЙ§ЪдбщЕїВщбаОПЃЌЗЂЯжПЩбЁдёКЏЪ§ФЃаЭ
ЕФЙиЯЕЃЌЭЈЙ§ЪдбщЕїВщбаОПЃЌЗЂЯжПЩбЁдёКЏЪ§ФЃаЭ![]() РДФтКЯ
РДФтКЯ![]() гы
гы![]() ЕФЙиЯЕЃЌИљОнвдЯТЪ§ОнЃК
ЕФЙиЯЕЃЌИљОнвдЯТЪ§ОнЃК
ВшвЖСП | 1 | 2 | 3 | 4 | 5 |
| 4.34 | 4.36 | 4.44 | 4.45 | 4.51 |
ПЩЧѓЕУyЙигкxЕФЛиЙщЗНГЬЮЊЃЈ ЃЉ

A.![]() B.
B.![]()
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com