
分析 (1)本题中已知tanα=2,由于$\frac{3sinα-2cosα}{sinα+cosα}$可以通过分子分母同除以cosα,将其变为用tanα表示,从而求出分式的值,故先用同角函数基本关系中的商数关系进行恒等变形,再代入值求分式的值;
(2)由已知中sinα+cosα=$\sqrt{2}$,两边平方后,根据sin2α+cos2α=1,可求出sinα•cosα=$\frac{1}{2}$,将tanα+cotα切化弦并通分后,结合sinα•cosα=$\frac{1}{2}$,即可得到答案.
解答 解:(1)由已知易知cosα≠0,
所以原式分子分母同时除以cosα,得$\frac{3sinα-2cosα}{sinα+cosα}$=$\frac{3tanα-2}{tanα+1}$=$\frac{3×2-2}{2+1}$=$\frac{4}{3}$.
(2)∵sinα+cosα=$\sqrt{2}$,
∴(sinα+cosα)2=1+2sinα•cosα=2,
∴sinα•cosα=$\frac{1}{2}$
∴tanα+cotα
=$\frac{sinα}{cosα}+\frac{cosα}{sinα}$
=$\frac{si{n}^{2}α+co{s}^{2}α}{sinαcosα}$
=$\frac{1}{\frac{1}{2}}$
=2.
点评 本题考查同角三角函数的基本关系,解题的关键是根据题设中分式的形式选择合适的公式进行恒等变形求值,此类齐次式,一般是通过分子分母同时除以余弦的方式将关于弦的分式变为关于切的分式.本题考查了转化化归的能力及观察的能力,利用三角公式进行运算的能力,利用公式计算是三角中的重要技能,要熟练掌握公式,灵活运用公式.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a${\;}^{-\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=0 | B. | a${\;}^{\frac{1}{2}}$÷a${\;}^{\frac{1}{3}}$=a${\;}^{\frac{5}{6}}$ | ||
| C. | (a3)2=a9 | D. | a${\;}^{\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x0>0,使得x0<sinx0 | |
| B. | “lna>lnb”是“10a>10b”的充要条件 | |
| C. | 若sinα≠$\frac{1}{2}$,则α≠$\frac{π}{6}$ | |
| D. | 若函数f(x)=x3+3ax2+bx+a2在x=-1有极值0,则a=2,b=9或a=1,b=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
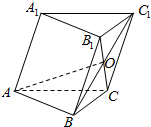 已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.
已知斜三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,∠BAA1=$\frac{2π}{3}$,∠CAA1=$\frac{π}{3}$,AB=AC=1,AA1=2,点O是B1C与BC1的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,6} | B. | {1,5} | C. | {1,6} | D. | {5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com