
 . D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.
. D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.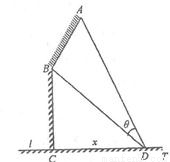
 求出其值即可.
求出其值即可. 当且仅当a=b时取等号的方法,求出tanθ的最大值,根据正切函数是单调增函数得到x的值表示出D的位置即可.
当且仅当a=b时取等号的方法,求出tanθ的最大值,根据正切函数是单调增函数得到x的值表示出D的位置即可.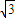 ,∠ABF=90°-60°=30°,
,∠ABF=90°-60°=30°, ,BF=4.5×cos30°=
,BF=4.5×cos30°=
 ,AE=CF=BC+BF=
,AE=CF=BC+BF=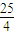
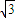 .
.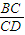 =
=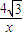 .
. 时,ED=x-
时,ED=x- ,tan∠ADC=
,tan∠ADC=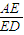 =
=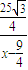 =
=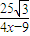 (如图1).
(如图1). 时,ED=
时,ED= -x,tan∠ADC=
-x,tan∠ADC=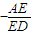 =
=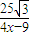 (如图2).
(如图2).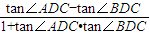 =
= =
= ,其中x>0且x≠
,其中x>0且x≠ .
. 时,tanθ=
时,tanθ= =
=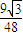 ,符合上式.
,符合上式.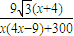 .x>0
.x>0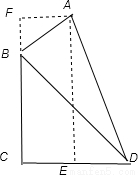 图2
图2
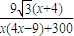 =
=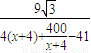 ,x>0.
,x>0. -41≥2
-41≥2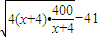 =39,当且仅当4(x+4)=
=39,当且仅当4(x+4)=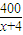 ,即x=6时取等号.
,即x=6时取等号.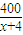 -41取最小值39.
-41取最小值39.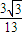 .
. )上是增函数,所以当x=6时,θ取得最大值.
)上是增函数,所以当x=6时,θ取得最大值.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
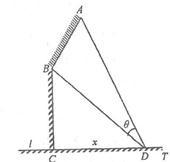 如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省高三5月模拟考试(二)文科数学试卷(解析版) 题型:解答题
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在直线与海岸线,的夹角为60°(海岸线看作直线),跑道上距离海岸线最近的点B到海岸线的距离BC=4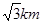 ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x> ),点D对跑道AB的视角为
),点D对跑道AB的视角为 .
.
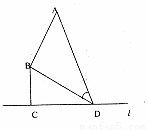
(1)将tan 表示为x的函数:
表示为x的函数:
(2)求点D的位置,使得 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高一下期中理科数学试卷(解析版) 题型:解答题
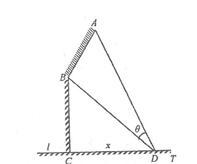
(本题满分15分)如图,某机场建在一个海湾的半岛上,飞机跑道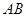 的长为4.5
的长为4.5 ,且跑道所在的直线与海岸线
,且跑道所在的直线与海岸线 的夹角为
的夹角为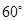 (海岸线可以看作是直线),跑道上离海岸线距离最近的点
(海岸线可以看作是直线),跑道上离海岸线距离最近的点 到海岸线的距离
到海岸线的距离 .
.
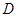 为海湾一侧海岸线
为海湾一侧海岸线 上的一点,设
上的一点,设 ,点
,点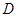 对跑道
对跑道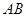 的视角为
的视角为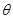 .
.
(1)
将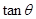 表示为
表示为 的函数;
的函数;
(2)已知常数 ,对于任意的
,对于任意的 ,
,
 ,等号成立当
,等号成立当
且仅当 ,求点
,求点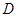 相对于垂足
相对于垂足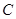 的位置,使
的位置,使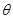 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60度(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60度(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离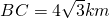 . D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.
. D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com