
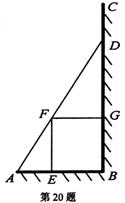
 如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值
如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值| S1 | S2 |
| S1 |
| S2 |
| π |
| 4 |
| S1 |
| S2 |
| 1 |
| 2 |
| π |
| 2 |
| FG |
| AB |
| DG |
| DB |
| t |
| a |
| atanθ-t |
| atanθ |
| atanθ |
| 1+tanθ |
| a2tan2θ |
| (1+tanθ)2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a2tan2θ |
| (1+tanθ)2 |
| S1 |
| S2 |
| (1+tanθ)2 |
| 2tanθ |
| S1 |
| S2 |
| 1 |
| 2 |
| 1 |
| tanθ |
| 1 |
| 2 |
| 1 |
| tanθ |
| π |
| 4 |
| π |
| 4 |
| S1 |
| S2 |


科目:高中数学 来源:2012届山东省日照市高三上学期测评理科数学试卷 题型:解答题
如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a, ,种草的面积为
,种草的面积为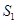 ,种花的面积为
,种花的面积为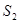 ,比值
,比值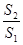 称为“规划和谐度”。
称为“规划和谐度”。
(I)试用 表示
表示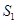 ,
,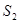 ;
;
(II)若 为定值,BC >AB。当
为定值,BC >AB。当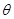 为何值时,“规划和谐度”有最小值?最小值是多少?
为何值时,“规划和谐度”有最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值
如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值 称为“规划和谐度”.
称为“规划和谐度”.查看答案和解析>>
科目:高中数学 来源:山东省月考题 题型:解答题
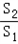 称为“规划和谐度”.
称为“规划和谐度”.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省德州市乐陵一中高三(上)期末数学复习训练试卷13(解析版) 题型:解答题
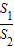 称为“规划和谐度”.
称为“规划和谐度”.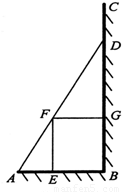
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com