
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 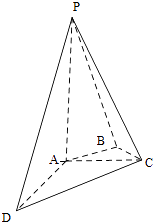
(1)证明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
【答案】
(1)[解法一] 如图,以A为原点,建立空间直角坐标系,则A(0,0,0),D(2,0,0),C(0,1,0),B(﹣ ![]() ,
, ![]() ,0),P(0,0,2).
,0),P(0,0,2).

证明:易得 ![]() =(0,1,﹣2),
=(0,1,﹣2), ![]() =(2,0,0),于是
=(2,0,0),于是 ![]()
![]() =0,所以PC⊥AD.
=0,所以PC⊥AD.
[解法二] 证明:由PA⊥平面ABCD,可得PA⊥AD,
又由AD⊥AC,PA∩AC=A,故AD⊥平面PAC,
又PC平面PAC,
所以PC⊥AD.
(2)[解法一] 解: ![]() =(0,1,﹣2),
=(0,1,﹣2), ![]() =(2,﹣1,0),设平面PCD的一个法向量为
=(2,﹣1,0),设平面PCD的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 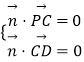 即
即 ![]()
取z=1,则以 ![]() =(1,2,1).又平面PAC的一个法向量为
=(1,2,1).又平面PAC的一个法向量为 ![]() =(1,0,0),于是cos<
=(1,0,0),于是cos< ![]() >=
>= ![]() =
= ![]() ,sin<
,sin< ![]() >=
>= ![]()
所以二面角A﹣PC﹣D的正弦值为 ![]()
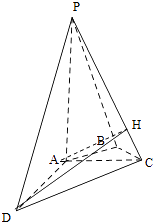
[解法二] 解:如图,作AH⊥PC于点H,连接DH,
由PC⊥AD,PC⊥AH,可得PC⊥平面ADH,因此DH⊥PC,从而∠AHD为二面角A﹣PC﹣D的平面角.
在RT△PAC中,PA=2,AC=1,所以AH= ![]() ,由(1)知,AD⊥AH,在RT△DAH中,DH=
,由(1)知,AD⊥AH,在RT△DAH中,DH= ![]() =
= ![]() ,因此sin∠AHD=
,因此sin∠AHD= ![]() =
= ![]() .所以二面角A﹣PC﹣D的正弦值为
.所以二面角A﹣PC﹣D的正弦值为 ![]()
(3)解法一:设E(0,0,h),其中h∈[0,2],由此得 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,h).由
,h).由 ![]() =(2,﹣1,0),故cos<
=(2,﹣1,0),故cos< ![]() >=
>= 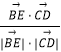 =
= 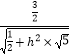 =
= ![]()
所以 ![]() =cos30°=
=cos30°= ![]() ,解得h=
,解得h= ![]() ,即AE=
,即AE= ![]() .
.
[解法二] 解:如图,因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,
设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.
由于BF∥CD,故∠AFB=∠ADC,在RT△DAC中,CD= ![]() ,sin∠ADC=
,sin∠ADC= ![]() ,故sin∠AFB=
,故sin∠AFB= ![]() .
.
在△AFB中,由 ![]() ,AB=
,AB= ![]() ,sin∠FAB=sin135°=
,sin∠FAB=sin135°= ![]() ,可得BF=
,可得BF= ![]() ,
,
由余弦定理,BF2=AB2+AF2﹣2ABAFcos∠FAB,得出AF= ![]() ,
,
设AE=h,在RT△EAF中,EF= ![]() =
= ![]() ,
,
在RT△BAE中,BE= ![]() =
= ![]() ,
,
在△EBF中,因为EF<BE,从而∠EBF=30°,
由余弦定理得到,cos30°= ![]() ,
,
解得h= ![]() ,
,
即AE= ![]() .
.

【解析】解法一(1)以A为原点,建立空间直角坐标系,通过得出 ![]()
![]() =0,证出PC⊥AD.(2)求出平面PCD,平面PCD的一个法向量,利用两法向量夹角求解.(3)设E(0,0,h),其中h∈[0,2],利用cos<
=0,证出PC⊥AD.(2)求出平面PCD,平面PCD的一个法向量,利用两法向量夹角求解.(3)设E(0,0,h),其中h∈[0,2],利用cos< ![]() >=cos30°=
>=cos30°= ![]() ,得出关于h的方程求解即可.解法二:(1)通过证明AD⊥平面PAC得出PC⊥AD.(2)作AH⊥PC于点H,连接DH,∠AHD为二面角A﹣PC﹣D的平面角.在RT△DAH中求解(3)因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.在△EBF中,因为EF<BE,从而∠EBF=30°,由余弦定理得出关于h的方程求解即可.
,得出关于h的方程求解即可.解法二:(1)通过证明AD⊥平面PAC得出PC⊥AD.(2)作AH⊥PC于点H,连接DH,∠AHD为二面角A﹣PC﹣D的平面角.在RT△DAH中求解(3)因为∠ADC<45°,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF,故∠EBF(或其补角)为异面直线BE与CD所成的角.在△EBF中,因为EF<BE,从而∠EBF=30°,由余弦定理得出关于h的方程求解即可.
【考点精析】解答此题的关键在于理解用空间向量求直线间的夹角、距离的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则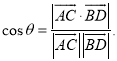 .
.


科目:高中数学 来源: 题型:
【题目】设F1,F2分别为椭圆C![]()
(1)若椭圆C上的点![]()
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M,N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM,PN的斜率都存在,并记为kPM,kPN时,那么kPM与kPN之积是与点P位置无关的定值,试写出双曲![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4及圆内一点P(2,5).
(1)求过P点的弦中,弦长最短的弦所在的直线方程;
(2)求过点M(5,0)与圆C相切的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() ,直线L:
,直线L:![]() .
.
⑴ 求证:对![]() ,直线L与圆C总有两个交点;
,直线L与圆C总有两个交点;
⑵ 求直线L与圆C截得的线段的最短长度,以及此时直线L的方程;;
⑶ 设直线L与圆C交于A、B两点若︱AB︱=![]() ,求L的倾斜角.
,求L的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校准备从高一年级的两个男生![]() 和三个女生
和三个女生![]() 中选择2个人去参加一项比赛.
中选择2个人去参加一项比赛.
(1)若从这5个学生中任选2个人,求这2个人都是女生的概率;
(2)若从男生和女生中各选1个人,求这2个人包括![]() ,但不包括
,但不包括![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记函数![]() 的定义域为D,若存在
的定义域为D,若存在![]() ,使
,使![]() 成立,则称以
成立,则称以![]() 为坐标的点是函数
为坐标的点是函数![]() 的图象上的“稳定点”.
的图象上的“稳定点”.
(1)若函数![]() 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
(2)已知定义在实数集R上的奇函数![]() 存在有限个“稳定点”,求证:
存在有限个“稳定点”,求证:![]() 必有奇数个“稳定点”.
必有奇数个“稳定点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  ,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
A.[4﹣2ln2,+∞)
B.( ![]() ,+∞)
,+∞)
C.(﹣∞,4﹣2ln2]
D.(﹣∞, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com