【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy 中，曲线C的参数方程为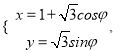
(
是参数,0≤
≤π),以O 为极点,以x 轴的正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线C 的极坐标方程；
(Ⅱ)直线l1,的极坐标方程是2psin(θ+
)+
=0,直线l2:θ =
与曲线C的交点为P，与直线l1的交点为Q,求线段PQ的长.
新思维假期作业寒假吉林大学出版社系列答案科目：高中数学 来源： 题型：
【题目】设点
，动圆
经过点
且和直线
相切，记动圆的圆心
的轨迹为曲线
.
（1）求曲线
的方程；
（2）设曲线
上一点
的横坐标为
，过
的直线交
于一点
，交
轴于点
，过点
作
的垂线交
于另一点
，若
是
的切线，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
为坐标原点，椭圆
： 
的左焦点是
，离心率为
，且
上任意一点
到
的最短距离为
.
（1）求
的方程；
（2）过点
的直线
（不过原点）与
交于两点
、
， 
为线段
的中点.
（i）证明：直线
与
的斜率乘积为定值；
（ii）求
面积的最大值及此时
的斜率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设命题
：函数
的定义域为
；命题
：关于
的方程
有实根.
（1）如果
是真命题，求实数
的取值范围.
（2）如果命题“
”为真命题，且“
”为假命题，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
、抛物线
的焦点均在
轴上， 
的中心和
的顶点均为原点
，平面上四个点
， 
， 
， 
中有两个点在椭圆
上，另外两个点在抛物线
上.
（1）求
的标准方程；
（2）是否存在直线
满足以下条件：①过
的焦点
；②与
交于
两点，且以
为直径的圆经过原点
.若存在，求出直线
的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.
(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】现采用随机模拟的方法估计一位射箭运动员三次射箭恰有两次命中的概率：先由计算机随机产生0到9之间取整数的随机数，指定1,2,3,4,5表示命中，6,7,8,9,0表示不命中，再以三个随机数为一组，代表三次射箭的结果，经随机模拟产生了如下20组随机数：
807 966 191 925 271 932 812 458 569 683
489 257 394 027 552 488 730 113 537 741
根据以上数据，估计该运动员三次射箭恰好有两次命中的概率为
A. 0.20 B. 0.25 C. 0.30 D. 0.50
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一装有水的直三棱柱
容器（厚度忽略不计），上下底面均为边长为5的正三角形，侧棱为10，侧面
水平放置，如图所示，点
， 
， 
， 
分别在棱
， 
， 
， 
上，水面恰好过点
， 
， 
， 
，且
．
（1）证明： 
；
（2）若底面
水平放置时，求水面的高．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在游学活动中，在
处参观的第
组同学通知在
处参观的第
组同学：第组正离开处向的东南方向游玩，速度约为
米/分钟．已知在的南偏西
方向且相距
米，第组同学立即出发沿直线行进并用
分钟与第组同学汇合．
（）设第组同学行进的方位角为
，求
．
（方位角：从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角）
（）求第组同学的行进速度为多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
