【题目】为调查某地区被隔离者是否需要社区非医护人员提供帮助，用简单随机抽样方法从该地区调查了500位被隔离者，结果如下：
性别 是否需要 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（1）估计该地区被隔离者中，需要社区非医护人员提供帮助的被隔离者的比例；
（2）能否有99%的把握认为该地区的被隔离者是否需要社区非医护人员提供帮助与性别有关？
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图1，在四边形
中，
，
，
，
，
，
是
上的点，
，
为
的中点．将
沿折起到
的位置，使得
，如图2．
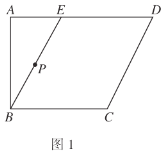
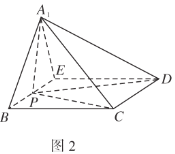
（1）求证：平面
平面
；
（2）点
在线段
上，当直线
与平面
所成角的正弦值为
时，求二面角
的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在新冠病毒疫情爆发期间，口罩成为了个人的必需品.已知某药店有4种不同类型的口罩
，
，
，
，其中型口罩仅剩1只（其余3种库存足够）.今甲、乙等5人先后在该药店各购买了1只口罩，统计发现他们恰好购买了3种不同类型的口罩，则所有可能的购买方式共有（ ）
A.330种B.345种C.360种D.375种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中国古代十进制的算筹计数法，在数学史上是一个伟大的创造，算筹实际上是一根根同长短的小木棍．如图，是利用算筹表示数1－9的一种方法．例如：3可表示为“≡”，26可表示为“=⊥”，现有6根算筹，据此表示方法，若算筹不能剩余，则可以用1－9这9个数字表示两位数中，能被3整除的概率是（ ）
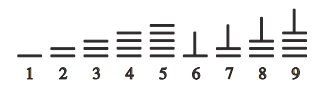
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
中，平面
底面
，
是等边三角形，底面是菱形，且
，
为棱
的中点，
为菱形的中心，下列结论正确的有（ ）
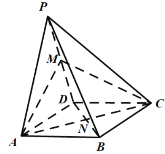
A.直线
与平面
平行B.直线与直线
垂直
C.线段
与线段
长度相等D.与所成角的余弦值为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于由正整数构成的数列
，若对任意
，
“且
，
也是中的项，则称为
数列”.设数列
|满足
，
..
（1）请给出一个的通项公式，使得既是等差数列也是“数列”，并说明理由；
（2）根据你给出的通项公式，设的前
项和为
，求满足
的正整数的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在我国，大学生就业压力日益严峻，伴随着政府政策引导与社会观念的转变，大学生创业意识，就业方向也悄然发生转变某大学生在国家提供的税收，担保贷款等很多方面的政策扶持下选择加盟某专营店自主
创业，该专营店统计了近五年来创收利润数
（单位：万元）与时间
（单位：年）的数据，列表如下：
| 1 | 2 | 3 | 4 | 5 |
| 2.4 | 2.7 | 4.1 | 6.4 | 7.9 |
（Ⅰ）依据表中给出的数据，是否可用线性回归模型拟合
与
的关系，请计算相关系数
并加以说明（计算结果精确到0.01）．（若
，则线性相关程度很高，可用线性回归模型拟合）：
（Ⅱ）该专营店为吸引顾客，特推出两种促销方案．
方案一：每满500元可减50元；
方案二：每满500元可抽奖一次，每次中奖的概率都为
，中奖就可以获得100元现金奖励，假设顾客每次抽奖的结果相互独立．
①某位顾客购买了1050元的产品，该顾客选择参加两次抽奖，求该顾客获得100元现金奖励的概率．
②某位顾客购买了1500元的产品，作为专营店老板，是希望该顾客直接选择返回150元现金，还是选择参加三次抽奖？说明理由
附：相关系数公式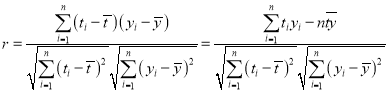
参考数据：
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
