
【题目】已知![]() .
.
(1)若![]() 在
在![]() 处有极值,求
处有极值,求![]() 的单调递增区间;
的单调递增区间;
(2)是否存在实数![]() ,使
,使![]() 在区间
在区间![]() 上的最小值是3,若存在,求出
上的最小值是3,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中点,N是CE的中点.
,M是AB的中点,N是CE的中点.
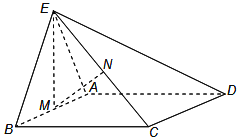
(1)求证:![]() ;
;
(2)求证:![]() 平面ADE;
平面ADE;
(3)求点A到平面BCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .直线
.直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .记点
.记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)已知直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与线段
处的切线与线段![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
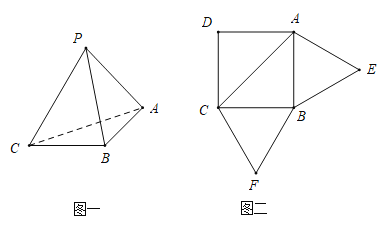
【题目】已知三棱锥![]() 的展开图如图二,其中四边形
的展开图如图二,其中四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com