
分析 (1)把方程x2+y2+x-6y+m=0化为圆的标准方程为(x+$\frac{1}{2}$)2+(y-3)2=$\frac{37}{4}$-m,故有$\frac{37}{4}$-m>0,由此解得m的范围.
(2)设P(x1,y1),Q(x2,y2).OP⊥OQ,故 x1•x2+y1•y2=0 ①,把直线x+2y-3=0代入圆的方程化简,利用根与系数的关系可得y1+y2=4,y1•y2=$\frac{12+m}{5}$,代入①求得m的值,即可得到圆C的方程.
解答 解:(1)方程x2+y2+x-6y+m=0即(x+$\frac{1}{2}$)2+(y-3)2=$\frac{37}{4}$-m,
∵方程表示的曲线是圆C,
∴$\frac{37}{4}$-m>0,解得m<$\frac{37}{4}$.
(2)设P(x1,y1),Q(x2,y2).∵OP⊥OQ,故 x1•x2+y1•y2=0 ①.
直线x+2y-3=0与圆C联立得5y2-20y+12+m=0,∴y1+y2=4,y1•y2=$\frac{12+m}{5}$.
∴x1•x2=(3-2y1)(3-2y2)=9-6(y1+y2)+4y1•y2.
代入①可得5y1•y2-6(y1+y2)+9=0,解得m=3,满足△>0.
圆C的方程为:(x+$\frac{1}{2}$)2+(y-3)2=$\frac{25}{4}$.
点评 本题主要考查二元二次方程表示圆的条件,圆的标准方程,直线和圆的位置关系以及弦长公式的应用,体现了分类讨论的数学思想,属于中档题.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
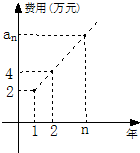 某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要支付设备的维修和工人工资等费用an的信息如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com