练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：


    喜爱打篮球

    不喜爱打篮球

    合计

    男生


    5


    女生

    10



    合计



    ５０

    已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为．

    （1）请将上面的列联表补充完整；

    （2）是否在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关？说明你的理由.下面的临界值表供参考：


    0.15

    0.10

    0.05

    0.025

    0.010

    0.005]

    0.001


    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    (参考公式：，其中)

    【答案】（1）列联表补充如下:


    喜爱打篮球

    不喜爱打篮球

    合计

    男生

    ２０

    ５

    ２５

    女生

    １０

    １５

    ２５

    合计

    ３０

    ２０

    ５０

    （2）犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关

    【解析】

    试题解：(1) 列联表补充如下：


    喜爱打篮球

    不喜爱打篮球

    合计

    男生

    ２０

    ５

    ２５

    女生

    １０

    １５

    ２５

    合计

    ３０

    ２０

    ５０

    （2）∵

    在犯错误的概率不超过0.5%的前提下认为喜爱打篮球与性别有关

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】曲线，直线关于直线对称的直线为，直线，与曲线分别交于点、和、，记直线的斜率为．

    （Ⅰ）求证：；

    （Ⅱ）当变化时，试问直线是否恒过定点？若恒过定点，求出该定点坐标；若不恒过定点，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某地有南北街道5条，东西街道5条，现在甲、乙、丙3名邮递员从该地西南角的邮局出发，送信到东北角的地，要求所走路程最短，设图中点，，是交叉路口，且路段由于修路不能通行.

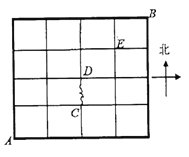
    （1）求甲从到共有多少种走法？（用数字作答）

    （2）求甲经过点的概率；

    （3）设3名邮递员恰有名邮递员经过点，求随机变量的概率分布和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

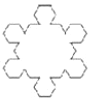
    【题目】如图，第1个图形由正三角形扩展而成，共12个顶点.第n个图形是由正n+2边形扩展而来 ，则第n+1个图形的顶点个数是 (　　)

    （1） （2）（3） （4）

    A. (2n+1)(2n+2)B. 3(2n+2)C. (n+2)(n+3)D. (n+3)(n+4)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”已成为当下热门的健身方式，小王的微信朋友圈内也有大量好友参与了“微信运动”，他随机选取了其中的人（男、女各人），记录了他们某一天的走路步数，并将数据整理如下：

    步量

    性别

    0~2000

    2001~5000

    5001~8000

    8001~10000

    >10000

    男

    1

    2

    3

    6

    8

    女

    0

    2

    10

    6

    2

    （1）已知某人一天的走路步数超过步被系统评定“积极型”，否则为“懈怠型”，根据题意完成下面的列联表，并据此判断能否有以上的把握认为“评定类型”与“性别”有关？

    积极型

    懈怠型

    总计

    男

    女

    总计

    附：，

    0.10

    0.05

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    （2）若小王以这位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布，现从小王的所有微信好友中任选人，其中每日走路不超过步的有人，超过步的有人，设，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥，底面为菱形，，为上的点，过的平面分别交，于点，，且平面.

    （1）证明：；

    （2）当为的中点，，与平面所成的角为，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】是定义在上的奇函数，且

    （1）求，的值；

    （2）判断函数的单调性（不需证明），并求使成立的实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某服装批发市场1-5月份的服装销售量与利润的统计数据如下表:

    月份

    1

    2

    3

    4

    5

    销售量 (万件)

    3

    6

    4

    7

    8

    利润 (万元)

    19

    34

    26

    41

    46

    （1）从这五个月的利润中任选2个，分别记为， ，求事件“， 均不小于30”的概率；

    （2）已知销售量与利润大致满足线性相关关系，请根据前4个月的数据，求出关于的线性回归方程；

    （3）若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元，则认为得到的利润的估计数据是理想的．请用表格中第5个月的数据检验由（2）中回归方程所得的第5个月的利润的估计数据是否理想．参考公式: ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，点在椭圆：上.若点，，且.

    （1）求椭圆的离心率；

    （2）设椭圆的焦距为4，，是椭圆上不同的两点，线段的垂直平分线为直线，且直线不与轴重合.

    ①若点，直线过点，求直线的方程；

    ② 若直线过点，且与轴的交点为，求点横坐标的取值范围.

    查看答案和解析>>

    同步练习册答案