
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
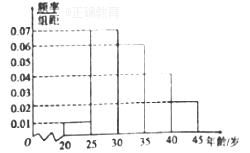
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】(2017·深圳二模)在“新零售”模式的背景下,某大型零售公司为推广线下分店,计划在S市的A区开设分店.为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y-0.05x2-1.4,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
参考公式: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知四棱锥![]() 的侧棱长与底面边长都相等,四边形
的侧棱长与底面边长都相等,四边形![]() 为正方形,点
为正方形,点![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

(2)如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于四个正数![]() ,如果
,如果![]() ,那么称
,那么称![]() 是
是![]() 的“下位序对”,
的“下位序对”,
(1)对于2,3,7,11,试求![]() 的“下位序对”;
的“下位序对”;
(2)设![]() 均为正数,且
均为正数,且![]() 是
是![]() 的“下位序对”,试判断
的“下位序对”,试判断![]() 之间的大小关系;
之间的大小关系;
(3)设正整数![]() 满足条件:对集合
满足条件:对集合![]() 内的每个
内的每个![]() ,总存在
,总存在![]() ,使得
,使得![]() 是
是![]() 的“下位序对”,且
的“下位序对”,且![]() 是
是![]() 的“下位序对”,求正整数
的“下位序对”,求正整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在定义域[﹣5,5]上满足f(x)﹣f(﹣x)=0,且f(3)=0,当x∈[0,5]时,f(x)的图象如图所示,则不等式xf(x)<0的解集是_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com