
【题目】若无穷数列![]() 满足:
满足:![]() 是正实数,当
是正实数,当![]() 时,
时,![]() ,则称
,则称![]() 是“
是“![]() -数列”.已知数列
-数列”.已知数列![]() 是“
是“![]() -数列”.
-数列”.
(Ⅰ)若![]() ,写出
,写出![]() 的所有可能值;
的所有可能值;
(Ⅱ)证明:![]() 是等差数列当且仅当
是等差数列当且仅当![]() 单调递减;
单调递减;
(Ⅲ)若存在正整数![]() ,对任意正整数
,对任意正整数![]() ,都有
,都有![]() ,证明:
,证明:![]() 是数列
是数列![]() 的最大项.
的最大项.
【答案】(1)-2,0,2,8.(2)见解析(3)见解析
【解析】分析:(Ⅰ)利用递推关系,根据分类讨论思想求解即可;(Ⅱ)当![]() 是等差数列时,利用反证法可证明
是等差数列时,利用反证法可证明![]() 单调递减,若
单调递减,若![]() 单调递减,当
单调递减,当![]() 单调递减时,对任意
单调递减时,对任意![]() ,
,![]() .又
.又![]() ,所以
,所以![]() ,从而
,从而![]() 是等差数列;(Ⅲ)利用反证法:假设
是等差数列;(Ⅲ)利用反证法:假设![]() 不是数列
不是数列![]() 的最大项,设
的最大项,设![]() 是使得
是使得![]() 的最小正整数,可得
的最小正整数,可得![]() 是
是![]() 的倍数,但
的倍数,但![]() ,故
,故![]() 不是
不是![]() 的倍数,相矛盾,从而可得结论.
的倍数,相矛盾,从而可得结论.
详解:(Ⅰ) -2,0,2,8.
(Ⅱ)证明:因为![]() ,所以
,所以![]() 或
或![]() .
.
当![]() 是等差数列时,假设
是等差数列时,假设![]() ,则
,则![]() .此时,
.此时,![]() ,而
,而![]() ,矛盾!所以
,矛盾!所以![]() .于是公差
.于是公差![]() ,所以
,所以![]() 单调递减.
单调递减.
当![]() 单调递减时,对任意
单调递减时,对任意![]() ,
,![]() .又
.又![]() ,所以
,所以![]() ,从而
,从而![]() 是等差数列.
是等差数列.
(Ⅲ)证明:假设![]() 不是数列
不是数列![]() 的最大项,设
的最大项,设![]() 是使得
是使得![]() 的最小正整数,则
的最小正整数,则
![]() ,
,
因此,![]() 是
是![]() 的倍数.
的倍数.
假设![]() ,
,![]() ,…,
,…,![]() 都是
都是![]() 的倍数,则
的倍数,则
![]()
![]() ,
,
因此,![]() 也是
也是![]() 的倍数.
的倍数.
由第二数学归纳法可知,对任意![]() ,
,![]() 都是
都是![]() 的倍数.
的倍数.
又存在正整数![]() ,对任意正整数
,对任意正整数![]() ,都有
,都有![]() ,
,
所以,存在正整数![]() ,
,![]() ,因而
,因而![]() 是
是![]() 的倍数.
的倍数.
但![]() ,故
,故![]() 不是
不是![]() 的倍数,矛盾!
的倍数,矛盾!
所以,![]() 是数列
是数列![]() 的最大项.
的最大项.


科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
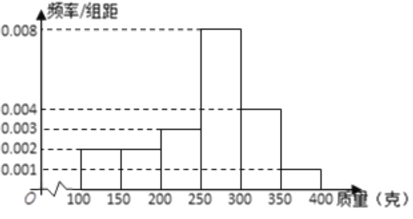
(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子中有形状、大小都相同的3只红球,2只白球,从中一次摸出2只球.
(1)求摸到的2只球颜色不同的概率:
(2)求摸到的2只球中至少有1只红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足![]() .
.
(1)若![]() ,求证:存在
,求证:存在![]() (a,b,c为常数),使数列
(a,b,c为常数),使数列![]() 是等比数列,并求出数列{an}的通项公式;
是等比数列,并求出数列{an}的通项公式;
(2)若an 是一个等差数列{bn}的前n项和,求首项a1的值与数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数为( )
①两个有共同始点且相等的向量,其终点可能不同;
②若非零向量![]() 与
与![]() 共线,则
共线,则![]() 、
、![]() 、
、![]() 、
、![]() 四点共线;
四点共线;
③若非零向量![]() 与
与![]() 共线,则
共线,则![]() ;
;
④四边形![]() 是平行四边形,则必有
是平行四边形,则必有![]() ;
;
⑤![]() ,则
,则![]() 、
、![]() 方向相同或相反.
方向相同或相反.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次“汉马”(武汉马拉松比赛的简称)全程比赛中,50名参赛选手(24名男选手和26名女选手)的成绩(单位:分钟)分别为数据![]() (成绩不为0).
(成绩不为0).
(Ⅰ)24名男选手成绩的茎叶图如图⑴所示,若将男选手成绩由好到差编为1~24号,再用系统抽样方法从中抽取6人,求其中成绩在区间![]() 上的选手人数;
上的选手人数;

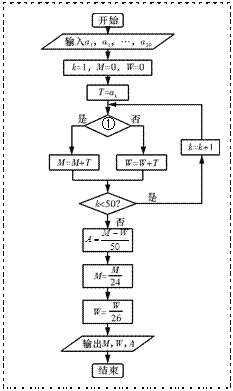
(Ⅱ)如图⑵所示的程序用来对这50名选手的成绩进行统计.为了便于区别性别,输入时,男选手的成绩数据用正数,女选手的成绩数据用其相反数(负数),请完成图⑵中空白的判断框①处的填写,并说明输出数值![]() 和
和![]() 的统计意义.
的统计意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com