
已知数列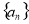 满足
满足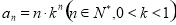 ,给出下列命题:
,给出下列命题:
①当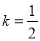 时,数列
时,数列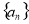 为递减数列
为递减数列
②当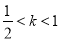 时,数列
时,数列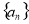 不一定有最大项
不一定有最大项
③当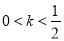 时,数列
时,数列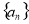 为递减数列
为递减数列
④当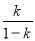 为正整数时,数列
为正整数时,数列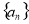 必有两项相等的最大项
必有两项相等的最大项
请写出正确的命题的序号____
科目:高中数学 来源:2013-2014学年安徽省合肥市高三第二次教学质量检测理科数学试卷(解析版) 题型:选择题
已知函数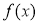 满足:对定义域内的任意
满足:对定义域内的任意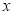 ,都有
,都有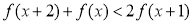 ,则函数
,则函数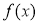 可以是( )
可以是( )
A.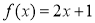 B.
B.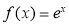 C.
C.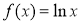 D.
D.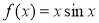
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试理科数学试卷(解析版) 题型:选择题
命题“若 ,则一元二次方程
,则一元二次方程 有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
A.0 B.2 C.4 D.不确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“江淮十校协作体”四月联考卷理科数学试卷(解析版) 题型:解答题
已知椭圆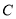 的中心在原点,焦点在
的中心在原点,焦点在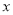 轴上,离心率为
轴上,离心率为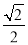 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线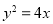 的焦点重合.
的焦点重合.
求椭圆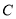 的方程;
的方程;
设椭圆的上顶点为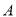 ,过点
,过点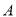 作椭圆
作椭圆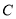 的两条动弦
的两条动弦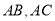 ,若直线
,若直线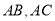 斜率之积为
斜率之积为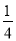 ,直线
,直线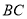 是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“江淮十校协作体”四月联考卷理科数学试卷(解析版) 题型:选择题
已知角 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴的非负半轴重合,终边在直线
轴的非负半轴重合,终边在直线 上,则
上,则 等于( )
等于( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“江淮十校协作体”四月联考卷文科数学试卷(解析版) 题型:选择题
如果 满足不等式组
满足不等式组 ,那么目标函数
,那么目标函数 的最小值是( )
的最小值是( )
A.-1 B.-3 C.-4 D.-9
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市蓟县高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
袋中装有若干个质地均匀大小一致的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球然后放回,若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(1)求摸球3次就停止的事件发生的概率;
(2)记摸到红球的次数为 ,求随机变量
,求随机变量 的分布列及其期望.
的分布列及其期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com