
【题目】设函数![]() ,
, ![]() .
.
(1) 关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有解,求
上有解,求![]() 的取值范围;
的取值范围;
(2) 当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD中,PD![]() 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD![]() DC,AB=AD=1,DC=2,PD=
DC,AB=AD=1,DC=2,PD=![]() ,M为棱PB的中点.
,M为棱PB的中点.
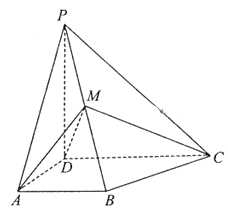
(1)证明:DM![]() 平面PBC;
平面PBC;
(2)求二面角A—DM—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,奇函数的个数为( ) ①y=x2sinx ②y=sinx , x∈ ![]() ③y=xcosx , x∈
③y=xcosx , x∈ ![]() ④y=tanx .
④y=tanx .
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2﹣ax(a∈R)
(1)a=3时,求函数f(x)的单调区间;
(2)若f(x)≤2x2恒成立,求实数a的取值范围;
(3)求证;lnn> ![]() +
+ ![]() +1
+1 ![]() +…+
+…+ ![]() (n∈N+)且n≥2.
(n∈N+)且n≥2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下命题正确的是( )
A.α,β都是第一象限角,若cosα>cosβ,则sinα>sinβ
B.α,β都是第二象限角,若sinα>sinβ,则tanα>tanβ
C.α,β都是第三象限角,若cosα>cosβ,则sinα>sinβ
D.α,β都是第四象限角,若sinα>sinβ,则tanα>tanβ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若对于任意的n∈N* , 都有Sn=2an﹣3n.
(1)求证{an+3}是等比数列
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正项数列{an}的前n项和为Sn , 且满足 ![]() .
.
(1)计算a1 , a2 , a3的值,并猜想{an}的通项公式;
(2)用数学归纳法证明{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com