
ΓΨΧβΡΩΓΩΈΣΝΥ―–ΨΩ≤ΜΆ§–‘±π‘Ύ¥ΠάμΕύ»ΈΈώ ±ΒΡ±μœ÷≤ν“λΘ§’ΌΦ·ΝΥΡ–≈°÷Ψ‘Η’ΏΗς200ΟϊΘ§“Σ«σΥϊΟ«Ά§ ±Άξ≥…ΕύΗω»ΈΈώΘ§Αϋά®ΫβΧβΓΔΕΝΒΊΆΦΓΔΫ”ΒγΜΑ.œ¬ΆΦ±μ ΨΝΥ÷Ψ‘Η’ΏΆξ≥…»ΈΈώΥυ–ηΒΡ ±ΦδΖ÷≤Φ.“‘œ¬Ϋα¬έΘ§Ε‘÷Ψ‘Η’ΏΆξ≥…»ΈΈώΥυ–ηΒΡ ±ΦδΖ÷≤ΦΆΦ±μάμΫβ’ΐ»ΖΒΡ «Θ® Θ©

ΔΌΉήΧεΩ¥≈°–‘¥ΠάμΕύ»ΈΈώΤΫΨυ”Ο ±ΗϋΕΧΘΜ
ΔΎΥυ”–≈°–‘¥ΠάμΕύ»ΈΈώΒΡΡήΝΠΕΦ“Σ”≈”ΎΡ––‘ΘΜ
ΔέΡ––‘ΒΡ ±ΦδΖ÷≤ΦΗϋΫ”Ϋϋ’ΐΧ§Ζ÷≤ΦΘΜ
Δή≈°–‘¥ΠάμΕύ»ΈΈώΒΡ”Ο ±ΈΣ’ΐ ΐΘ§Ρ––‘¥ΠάμΕύ»ΈΈώΒΡ”Ο ±ΈΣΗΚ ΐ.
A.ΔΌΔήB.ΔΎΔέC.ΔΌΔέD.ΔΎΔή
ΓΨ¥πΑΗΓΩC
ΓΨΫβΈωΓΩ
ΆΦœώΈΣΕ‘÷Ψ‘Η’ΏΆξ≥…»ΈΈώΥυ–ηΒΡ ±ΦδΖ÷≤ΦΆΦ±μ,άϊ”ΟΆΦœώ“ά¥ΈΖ÷ΈωΦ¥Ω…
”…ΆΦ,≈°–‘¥ΠάμΕύ»ΈΈώ”Ο ±÷ς“ΣΦ·÷–‘Ύ2ΒΫ3Ζ÷÷”,Ρ––‘¥ΠάμΕύ»ΈΈώ”Ο ±÷ς“ΣΦ·÷–‘Ύ3ΒΫ4Ζ÷÷”,Ι ΉήΧεά¥Ω¥≈°–‘¥ΠάμΕύ»ΈΈώ”Ο ±ΗϋΕΧ,Ι ΔΌ’ΐ»ΖΘΜ
≈°–‘÷–“≤”–¥ΠάμΕύ»ΈΈώ”Ο ±‘Ύ5Ζ÷÷”ΒΡ,≤Δ≤Μ «Υυ”–≈°–‘¥ΠάμΕύ»ΈΈώΡήΝΠΕΦ“Σ”≈”ΎΡ––‘,Ι ΔΎ¥μΈσΘΜ
¥”ΆΦœώ…œά¥Ω¥Ρ––‘ΒΡ ±ΦδΖ÷≤ΦΗϋΫ”Ϋϋ’ΐΧ§Ζ÷≤Φ,Ι Δέ’ΐ»ΖΘΜ
Ρ––‘ΓΔ≈°–‘¥ΠάμΕύ»ΈΈώΒΡ”Ο ±ΨυΈΣ’ΐ ΐ,Ι Δή¥μΈσΘΜ
Ήέ…œ,ΔΌΔέ’ΐ»Ζ,
Ι ―Γ:C



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©![]() »τΖΫ≥Χ2[fΘ®xΘ©]2©¹5tfΘ®xΘ©+3t2ΘΫ0«Γ”–4Ηω≤ΜΆ§ΒΡ ΒΗυΘ§‘ρ Β ΐtΒΡ»Γ÷ΒΖΕΈßΈΣΘ®≤ΈΩΦ ΐΨίΘΚln2Γ÷0.6931Θ©Θ® Θ©
»τΖΫ≥Χ2[fΘ®xΘ©]2©¹5tfΘ®xΘ©+3t2ΘΫ0«Γ”–4Ηω≤ΜΆ§ΒΡ ΒΗυΘ§‘ρ Β ΐtΒΡ»Γ÷ΒΖΕΈßΈΣΘ®≤ΈΩΦ ΐΨίΘΚln2Γ÷0.6931Θ©Θ® Θ©
A.Θ®![]() Θ§
Θ§![]() Θ©
Θ©
B.Θ®![]() Θ§
Θ§![]() Θ©
Θ©
C.Θ®![]() Θ§2©¹2ln2Θ©Γ»Θ®
Θ§2©¹2ln2Θ©Γ»Θ®![]() Θ§1Θ©
Θ§1Θ©
D.Θ®![]() Θ§2©¹1n2Θ©
Θ§2©¹1n2Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η«ζœΏEΒΡΖΫ≥ΧΈΣ![]() 1Θ§Ε·ΒψAΘ®mΘ§nΘ©Θ§BΘ®©¹mΘ§nΘ©Θ§CΘ®©¹mΘ§©¹nΘ©Θ§DΘ®mΘ§©¹nΘ©‘ΎE…œΘ§Ε‘”ΎΫα¬έΘΚΔΌΥΡ±Ώ–ΈABCDΒΡΟφΜΐΒΡΉν–Γ÷ΒΈΣ48ΘΜΔΎΥΡ±Ώ–ΈABCDΆβΫ”‘≤ΒΡΟφΜΐΒΡΉν–Γ÷ΒΈΣ25Π–.œ¬ΟφΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ©
1Θ§Ε·ΒψAΘ®mΘ§nΘ©Θ§BΘ®©¹mΘ§nΘ©Θ§CΘ®©¹mΘ§©¹nΘ©Θ§DΘ®mΘ§©¹nΘ©‘ΎE…œΘ§Ε‘”ΎΫα¬έΘΚΔΌΥΡ±Ώ–ΈABCDΒΡΟφΜΐΒΡΉν–Γ÷ΒΈΣ48ΘΜΔΎΥΡ±Ώ–ΈABCDΆβΫ”‘≤ΒΡΟφΜΐΒΡΉν–Γ÷ΒΈΣ25Π–.œ¬ΟφΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ©
A.ΔΌ¥μΘ§ΔΎΕ‘B.ΔΌΕ‘Θ§ΔΎ¥μC.ΔΌΔΎΕΦ¥μD.ΔΌΔΎΕΦΕ‘
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘≤÷υΒΡ÷αΫΊΟφ![]() «±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–ΈΘ§Βψ
«±Ώ≥ΛΈΣ2ΒΡ’ΐΖΫ–ΈΘ§Βψ![]() «‘≤ΜΓ
«‘≤ΜΓ![]() …œΒΡ“ΜΕ·ΒψΘ®≤Μ”κ
…œΒΡ“ΜΕ·ΒψΘ®≤Μ”κ![]() ÷ΊΚœΘ©Θ§Βψ
÷ΊΚœΘ©Θ§Βψ![]() «‘≤ΜΓ
«‘≤ΜΓ![]() ΒΡ÷–ΒψΘ§«“Βψ
ΒΡ÷–ΒψΘ§«“Βψ![]() ‘ΎΤΫΟφ
‘ΎΤΫΟφ![]() ΒΡΝΫ≤ύ.
ΒΡΝΫ≤ύ.
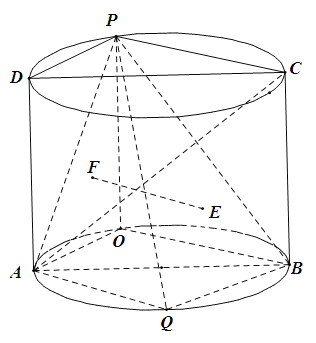
Θ®1Θ©÷ΛΟςΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©…ηΒψ![]() ‘ΎΤΫΟφ
‘ΎΤΫΟφ![]() …œΒΡ…δ”ΑΈΣΒψ
…œΒΡ…δ”ΑΈΣΒψ![]() Θ§Βψ
Θ§Βψ![]() Ζ÷±π «
Ζ÷±π «![]() ΚΆ
ΚΆ![]() ΒΡ÷Ί–ΡΘ§Β±»ΐάβΉΕ
ΒΡ÷Ί–ΡΘ§Β±»ΐάβΉΕ![]() ΧεΜΐΉν¥σ ±Θ§ΜΊ¥πœ¬Ν–Έ Χβ.
ΧεΜΐΉν¥σ ±Θ§ΜΊ¥πœ¬Ν–Έ Χβ.
Θ®ΔΓΘ©÷ΛΟςΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔΔΘ©«σΤΫΟφ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…ΕΰΟφΫ«ΒΡ’ΐœ“÷Β.
Υυ≥…ΕΰΟφΫ«ΒΡ’ΐœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
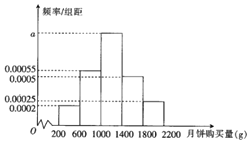
ΓΨΧβΡΩΓΩ2018Ρξ÷–«οΫΎΒΫά¥÷°Φ Θ§Ρ≥≥§ –ΈΣΝΥΫβ÷–«οΫΎΤΎΦ䑬±ΐΒΡœζ έΝΩΘ§Ε‘ΤδΥυ‘Ύœζ έΖΕΈßΡΎΒΡ1000ΟϊœϊΖ―’Ώ‘Ύ÷–«οΫΎΤΎΦδΒΡ‘¬±ΐΙΚ¬ρΝΩ![]() ΒΞΈΜΘΚ
ΒΞΈΜΘΚ![]() Ϋχ––ΝΥΈ ΨμΒς≤ιΘ§ΒΟΒΫ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
Ϋχ––ΝΥΈ ΨμΒς≤ιΘ§ΒΟΒΫ»γœ¬ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘΚ
![]() «σΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–aΒΡ÷ΒΘΜ
«σΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–aΒΡ÷ΒΘΜ
![]() “‘ΤΒ¬ ΉςΈΣΗ≈¬ Θ§ ‘«σœϊΖ―’Ώ‘¬±ΐΙΚ¬ρΝΩ‘Ύ
“‘ΤΒ¬ ΉςΈΣΗ≈¬ Θ§ ‘«σœϊΖ―’Ώ‘¬±ΐΙΚ¬ρΝΩ‘Ύ![]() ΒΡΗ≈¬ ΘΜ
ΒΡΗ≈¬ ΘΜ
![]() “―÷ΣΗΟ≥§ –Υυ‘Ύœζ έΖΕΈßΡΎ”–20Άρ»ΥΘ§≤Δ«“ΗΟ≥§ –ΟΩΡξΒΡœζ έΖίΕν‘Φ’ΦΗΟ –≥ΓΉήΝΩΒΡ
“―÷ΣΗΟ≥§ –Υυ‘Ύœζ έΖΕΈßΡΎ”–20Άρ»ΥΘ§≤Δ«“ΗΟ≥§ –ΟΩΡξΒΡœζ έΖίΕν‘Φ’ΦΗΟ –≥ΓΉήΝΩΒΡ![]() Θ§«κΗυΨί’β1000ΟϊœϊΖ―’ΏΒΡ»ΥΨυ‘¬±ΐΙΚ¬ρΝΩΙάΦΤΗΟ≥§ –”ΠΉΦ±ΗΕύ…ΌΕ÷‘¬±ΐ«ΓΚΟΡή¬ζΉψ –≥Γ–η«σ
Θ§«κΗυΨί’β1000ΟϊœϊΖ―’ΏΒΡ»ΥΨυ‘¬±ΐΙΚ¬ρΝΩΙάΦΤΗΟ≥§ –”ΠΉΦ±ΗΕύ…ΌΕ÷‘¬±ΐ«ΓΚΟΡή¬ζΉψ –≥Γ–η«σ![]() ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Ά§“ΜΉιΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μ
ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Ά§“ΜΉιΒΡ ΐΨί”ΟΗΟΉι«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μ![]() ΘΩ
ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() ΈΣ±Ώ
ΈΣ±Ώ![]() ΒΡ÷–ΒψΘ§“‘
ΒΡ÷–ΒψΘ§“‘![]() ΈΣ’έΚέΑ―
ΈΣ’έΚέΑ―![]() ’έΤπΘ§ ΙΒψ
’έΤπΘ§ ΙΒψ![]() ΒΫ¥οΒψ
ΒΫ¥οΒψ![]() ΒΡΈΜ÷ΟΘ§«“ ΙΤΫΟφ
ΒΡΈΜ÷ΟΘ§«“ ΙΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() .
.
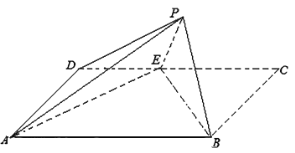
Θ®1Θ©÷ΛΟςΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΒψ![]() ΒΫΤΫΟφ
ΒΫΤΫΟφ![]() ΒΡΨύάκ.
ΒΡΨύάκ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ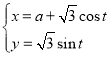 Θ®
Θ®![]() ΈΣ≤Έ ΐΘ§
ΈΣ≤Έ ΐΘ§![]() Θ©Θ§“‘Ήχ±ξ‘≠Βψ
Θ©Θ§“‘Ήχ±ξ‘≠Βψ![]() ΈΣΦΪΒψΘ§“‘
ΈΣΦΪΒψΘ§“‘![]() ÷α’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ
÷α’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ![]() …œ“ΜΒψ
…œ“ΜΒψ![]() ΒΡΦΪΉχ±ξΈΣ
ΒΡΦΪΉχ±ξΈΣ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() .
.
Θ®1Θ©«σ«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
ΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©…ηΒψ![]() ‘Ύ
‘Ύ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ®“λ”ΎΦΪΒψΘ©Θ§»τ
…œΘ®“λ”ΎΦΪΒψΘ©Θ§»τ![]() ΥΡΒψ“ά¥Έ‘ΎΆ§“ΜΧθ÷±œΏ
ΥΡΒψ“ά¥Έ‘ΎΆ§“ΜΧθ÷±œΏ![]() …œΘ§«“
…œΘ§«“![]() ≥…Β»±» ΐΝ–Θ§«σ
≥…Β»±» ΐΝ–Θ§«σ![]() ΒΡΦΪΉχ±ξΖΫ≥Χ.
ΒΡΦΪΉχ±ξΖΫ≥Χ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() ΈΣ’ΐ Β ΐ.
ΈΣ’ΐ Β ΐ.
(1)»τ≤ΜΒ» Ϋ![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
(2)Β±![]() ±Θ§÷ΛΟς
±Θ§÷ΛΟς![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΥΡάβΉΕ÷–![]() Θ§ΒΉΟφ
Θ§ΒΉΟφ![]() ΈΣΝβ–ΈΘ§
ΈΣΝβ–ΈΘ§![]() Θ§
Θ§![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§![]() ΓΔ
ΓΔ![]() Ζ÷±π «
Ζ÷±π «![]() ΓΔ
ΓΔ![]() …œΒΡ÷–ΒψΘ§÷±œΏ
…œΒΡ÷–ΒψΘ§÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΈΣ
Υυ≥…Ϋ«ΒΡ’ΐœ“÷ΒΈΣ![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ
‘Ύ![]() …œ“ΤΕ·.
…œ“ΤΕ·.
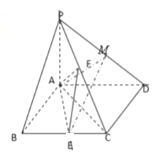
Θ®ΔώΘ©÷ΛΟςΘΚΈό¬έΒψ![]() ‘Ύ
‘Ύ![]() …œ»γΚΈ“ΤΕ·Θ§ΕΦ”–ΤΫΟφ
…œ»γΚΈ“ΤΕ·Θ§ΕΦ”–ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©«σΒψ![]() «ΓΈΣ
«ΓΈΣ![]() ΒΡ÷–Βψ ±Θ§ΕΰΟφΫ«
ΒΡ÷–Βψ ±Θ§ΕΰΟφΫ«![]() ΒΡ”ύœ“÷Β.
ΒΡ”ύœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com