练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆经过点离心率.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）经过椭圆左焦点的直线(不经过点且不与轴重合)与椭圆交于两点，与直线:交于点，记直线的斜率分别为.则是否存在常数，使得向量 共线？若存在求出的值；若不存在，说明理由.

    【答案】（1）；（2）2.

    【解析】

    （1）根据椭圆经过点，离心率，结合性质 ，列出关于 、 、的方程组，求出 、，即可得结果；（2）直线的方程为， 代入椭圆方程整理得，求得的坐标为，求出 ,利用韦达定理化简可得，从而可得结果.

    （1）由在椭圆上， .①

    由已知得，

    又， .②

    ②代入①解得.

    椭圆的方程为.

    （2）假设存在常数，使得向量共线，

    ，即.

    由题意可设的斜率为，

    则直线的方程为，③

    代入椭圆方程并整理，得，

    设，则有

    ，.④

    在方程③中令得，的坐标为.

    从而，，.

    , ⑤

    ④代入⑤得，

    又， .

    故存在常数符合题意.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论函数的单调性；

    （2）当a=1时，若关于的不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为常数，是自然对数的底数），曲线在点处的切线与轴平行.

    （Ⅰ）求的值；

    （Ⅱ）求的单调区间；

    （Ⅲ）设,其中为的导函数.证明：对任意.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足，且．

    (1)求证：数列是等差数列，并求出数列的通项公式；

    (2)求数列的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆的离心率，抛物线的焦点恰好是椭圆的右焦点．

    （1）求椭圆的标准方程；

    （2）过点作两条斜率都存在的直线，设与椭圆交于两点，与椭圆交于两点，若是与的等比中项，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四面体ABCD中，平面DAC⊥底面ABC，，AD＝CD＝，O是AC的中点，E是BD的中点．

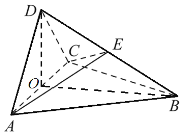
    （1）证明：DO⊥底面ABC；

    （2）求二面角D-AE-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．

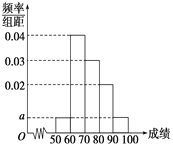
    (1)求图中a的值；

    (2)根据频率分布直方图，估计这100名学生语文成绩的平均分；

    (3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.

    分数段

    [50,60)

    [60,70)

    [70,80)

    [80,90)

    x∶y

    1∶1

    2∶1

    3∶4

    4∶5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的离心率为，且与抛物线交于，两点， （为坐标原点）的面积为．

    （1）求椭圆的方程；

    （2）如图，点为椭圆上一动点（非长轴端点），为左、右焦点，的延长线与椭圆交于点，的延长线与椭圆交于点，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市为鼓励人们绿色出行，乘坐地铁，地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策，不超过站的地铁票价如下表：

    乘坐站数

    票价（元）

    现有甲、乙两位乘客同时从起点乘坐同一辆地铁，已知他们乘坐地铁都不超过站.甲、乙乘坐不超过站的概率分别为， ；甲、乙乘坐超过站的概率分别为， .

    （1）求甲、乙两人付费相同的概率；

    （2）设甲、乙两人所付费用之和为随机变量，求的分布列和数学期望.

    查看答案和解析>>

    同步练习册答案