Question

16．已知圆O：x²+y²=16，圆O与x轴交于A，B两点，过点B的圆的切线为l，P是圆上异于A，B的一点，PH垂直于x轴，垂足为H，E是PH的中点，延长AP，AE分别交l于F，C．
（1）若点$P（-2，\;2\sqrt{3}）$，求以FB为直径的圆M的方程，并判断P是否在圆M上；
（2）当P在圆O上运动时，试判断直线PC与圆O的位置关系．

Answer 1

分析 （1）先确定直线AP的方程为y=$-\frac{\sqrt{3}}{3}（x-4）$，求得F（-4，$\frac{8\sqrt{3}}{3}$），确定直线AE的方程为y=$-\frac{\sqrt{3}}{6}（x-4）$，求得C（-4，$\frac{4\sqrt{3}}{3}$），由此可得圆的方程；
（2）设P（x₀，y₀），则E（x₀，$\frac{{y}_{0}}{2}$），求得直线AE的方程，进而可确定直线PC的斜率，由此即可证得直线PC与圆O相切．

解答 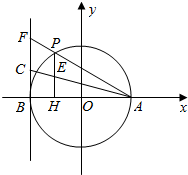（1）解：由$P（-2，\;2\sqrt{3}）$，A（4，0），得
直线AP的方程为y=$-\frac{\sqrt{3}}{3}（x-4）$，
令x=-4，得F（-4，$\frac{8\sqrt{3}}{3}$），
由E（-2，$\sqrt{3}$），A（4，0），则直线AE的方程为y=$-\frac{\sqrt{3}}{6}（x-4）$，
令x=-4，得C（-4，$\frac{4\sqrt{3}}{3}$），
∴C为线段FB的中点，以FB为直径的圆恰以C为圆心，半径等于$\frac{4\sqrt{3}}{3}$．
∴圆M的方程为$（x+4）^{2}+（y-\frac{4\sqrt{3}}{3}）^{2}=\frac{16}{3}$，且P在圆上；
（2）证明：设P（x₀，y₀），则E（x₀，$\frac{{y}_{0}}{2}$），则直线AE的方程为y=$\frac{{y}_{0}（x-4）}{2（{x}_{0}-4）}$，
在此方程中令x=-4，得C（-4，$-\frac{4{y}_{0}}{{x}_{0}-4}$），
直线PC的斜率为$\frac{{y}_{0}+\frac{4{y}_{0}}{{x}_{0}-4}}{{x}_{0}+4}=\frac{{x}_{0}{y}_{0}}{{{x}_{0}}^{2}-16}$=$-\frac{{x}_{0}}{{y}_{0}}$，
若x₀=0，则此时PC与y轴垂直，即PC⊥OP；
若x₀≠0，则此时直线OP的斜率为$\frac{{y}_{0}}{{x}_{0}}$，
∵$\frac{{y}_{0}}{{x}_{0}}•（-\frac{{x}_{0}}{{y}_{0}}）=-1$，
∴PC⊥OP．
∴直线PC与圆O相切．

点评 本题考查直线与圆的位置关系，考查圆的方程，解题的关键是确定圆的圆心与半径，利用斜率关系确定直线与圆相切，是中档题．