
���� ����������ԲQ�ij��᳤Ϊ2$\sqrt{2}$�����a=$\sqrt{2}$����P��x0��y0����ͨ��ֱ��PA��OM��б��֮����Ϊ��-$\frac{1}{2}$���������b�����ɵõ���Բ���̣�
����ֱ�߷��̴�����Բ���̣��ɴ�����Τ�ﶨ�����е����깫ʽ��ֱ�߷��̡��ҳ���ʽ��������߶�AB����ȡֵ��Χ��
��� �⣺�����������֪2a=2$\sqrt{2}$����a=$\sqrt{2}$����P��x0��y0����
��ֱ��PA��OM��б��֮����Ϊ-$\frac{1}{2}$����$\frac{\frac{{y}_{0}}{2}}{\frac{{x}_{0}+\sqrt{2}}{2}}$��$\frac{{y}_{0}}{{x}_{0}-\sqrt{2}}$=-$\frac{1}{2}$��
��$\frac{{x}_{0}^{2}}{2}$+${y}_{0}^{2}$=1��
��b=1��
��ԲC�ķ���$\frac{{x}^{2}}{2}+{y}^{2}=1$��
������ֱ��l��y=k��x+1����A��x1��y1����B��x2��y2����
����ֱ������Բ���̣�$\left\{\begin{array}{l}{y=k��x+1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$���ã���2k2+1��x2+4k2x+2k2-2=0��
��x1+x2=-$\frac{4{k}^{2}}{2{k}^{2}+1}$��x1x2=$\frac{2{k}^{2}-2}{2{k}^{2}+1}$��
��y1+y2=k��x1+x2+2��=$\frac{2k}{2{k}^{2}+1}$��
��AB�е�Q��-$\frac{2{k}^{2}}{2{k}^{2}+1}$��$\frac{k}{2{k}^{2}+1}$����
QNֱ�߷���Ϊ��y-$\frac{k}{2{k}^{2}+1}$=-$\frac{1}{k}$��x+$\frac{2{k}^{2}}{2{k}^{2}+1}$��=-$\frac{1}{k}$x-$\frac{2k}{2{k}^{2}+1}$��
��N��-$\frac{{k}^{2}}{2{k}^{2}+1}$��0��������֪��-$\frac{1}{4}$��-$\frac{{k}^{2}}{2{k}^{2}+1}$��0��
��0��2k2��1��
��|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{��-\frac{4{k}^{2}}{2{k}^{2}+1}��^{2}-4��\frac{2{k}^{2}-2}{2{k}^{2}+1}}$
=$\sqrt{1+{k}^{2}}$•$\frac{2\sqrt{2}\sqrt{1+{k}^{2}}}{2{k}^{2}+1}$=$\sqrt{2}$��1+$\frac{1}{2{k}^{2}+1}$����
��$\frac{1}{2}$����12k2+1��1��
��|AB|�ʣ�$\frac{3\sqrt{2}}{2}$��2$\sqrt{2}$����
�߶�AB����ȡֵ��Χ��$\frac{3\sqrt{2}}{2}$��2$\sqrt{2}$����
���� ���⿼����Բ���̡��߶γ���ȡֵ��Χ����������Բ��ֱ������Բ��λ�ù�ϵ��Ӧ�ã�����������֤�����������������������ת������˼�룬����ʱҪע��Τ�ﶨ�����е����깫ʽ��ֱ�߷��̡��ҳ���ʽ�ĺ������ã������е��⣮


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1511 | B�� | 1515 | C�� | 1521 | D�� | 1523 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | a��c��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ca��cb | B�� | ac��bc | C�� | $\frac{a}{a-c}��\frac{b}{b-c}$ | D�� | logac��logbc |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
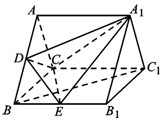 ��ͼ����������ABC-A1B1C1�У������ABC�ǵȱ������Σ���AA1��ƽ��ABC��DΪAB���е㣮
��ͼ����������ABC-A1B1C1�У������ABC�ǵȱ������Σ���AA1��ƽ��ABC��DΪAB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
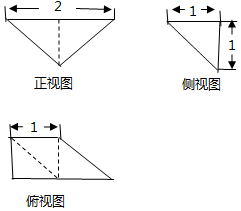 ij�����������ͼ��ͼ��ʾ����λ��cm������ü����������ǣ�������
ij�����������ͼ��ͼ��ʾ����λ��cm������ü����������ǣ�������| A�� | $\frac{1}{2}c{m^3}$ | B�� | 1cm3 | C�� | $\frac{3}{2}c{m^3}$ | D�� | 3cm3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��$\frac{1}{4}$] | B�� | [$\frac{1}{4}$��1] | C�� | [-2��$\frac{1}{4}$] | D�� | [$\frac{1}{3}$��1] |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com