Question

【题目】函数y=的图象与函数y=2sinπx（﹣2≤x≤4）的图象所有交点的横坐标之和等于（　　）
A.2
B.4
C.6
D.8

Answer 1

【答案】D
【解析】函数y1= ， y2=2sinπx的图象有公共的对称中心（1，0），作出两个函数的图象如图
当1＜x≤4时，y1＜0
而函数y2在（1，4）上出现1.5个周期的图象，
在和上是减函数；
在和上是增函数．
∴函数y1在（1，4）上函数值为负数，且与y2的图象有四个交点E、F、G、H
相应地，y1在（﹣2，1）上函数值为正数，且与y2的图象有四个交点A、B、C、D
且：xA+xH=xB+xG═xC+xF=xD+xE=2，故所求的横坐标之和为8
故选D.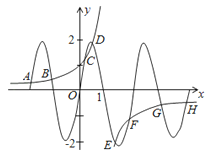

y1=的图象由奇函数y=的图象向右平移1个单位而得，所以它的图象关于点（1，0）中心对称，再由正弦函数的对称中心公式，可得函数y2=2sinπx的图象的一个对称中心也是点（1，0），故交点个数为偶数，且每一对对称点的横坐标之和为2．由此不难得到正确答案。