
(本小题满分12分)
如图,四棱锥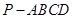 中,底面
中,底面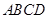 为矩形,
为矩形,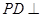 平面
平面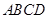 ,点
,点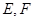 分别是
分别是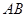 和
和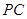 的中点.
的中点.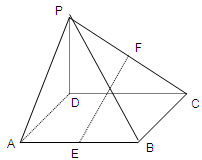
求证: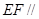 平面
平面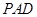 ;
;
若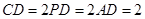 , 四棱锥
, 四棱锥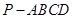 外接球的表面积.
外接球的表面积.
(1)取PD的中点G,连接FG,GA,GF//DC,GF=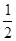 DC,AE=
DC,AE=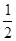 AB,矩形ABCD中,AB//DC,AB=DC,∴GF//AE,GF=AE?∴四边形AEFG是平行四边形,EF//AG,EF在平面PDA外,AG在平面PDA内,
AB,矩形ABCD中,AB//DC,AB=DC,∴GF//AE,GF=AE?∴四边形AEFG是平行四边形,EF//AG,EF在平面PDA外,AG在平面PDA内,
∴EF//平面PDA.(2)6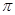
解析试题分析:(1)取PD的中点G,连接FG,GA,由G、F分别是PD、PC的中点,知GF是△PDC的中位线,
GF//DC,GF=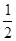 DC,
DC,
E是AB中点,AE=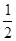 AB,
AB,
矩形ABCD中,AB//DC,AB=DC,
∴GF//AE,GF=AE? ……………………3分
∴四边形AEFG是平行四边形,EF//AG,
EF在平面PDA外,AG在平面PDA内,
∴EF//平面PDA. ……………………6分
(2)由图易知AB⊥平面PAD,四棱锥P-ABCD的 外接球即以DP,DA,DC为棱的长方体的外接球。
∴R=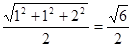 ,∴S=4
,∴S=4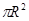 =6
=6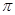 。 ……………………12分
。 ……………………12分
考点:线面平行的判定及锥体的外接球
点评:本题在证明线面平行时充分利用已知中出现的中点作出三角形中位线即可实现直线间的平行,此三棱锥是长方体一部分,其外接球转化为长方体外接球求解较容易


科目:高中数学 来源: 题型:解答题
如图(1),在等腰直角三角形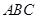 中,
中,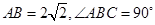 ,点
,点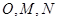 分别为线段
分别为线段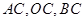 的中点,将
的中点,将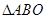 和
和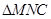 分别沿
分别沿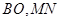 折起,使二面角
折起,使二面角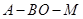 和二面角
和二面角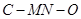 都成直二面角,如图(2)所示。
都成直二面角,如图(2)所示。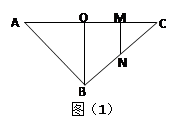

(1)求证: 面
面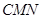 ;
;
(2)求平面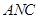 与平面
与平面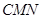 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)求点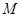 到平面
到平面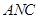 的距离。
的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图是从上下底面处在水平状态下的棱长为 的正方体
的正方体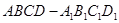 中分离出来的:
中分离出来的: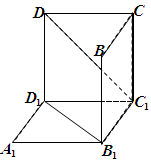
(1)试判断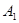 是否在平面
是否在平面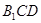 内;(回答是与否)
内;(回答是与否)
(2)求异面直线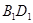 与
与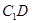 所成的角;
所成的角;
(3)如果用图示中这样一个装置来盛水,那么最多可以盛多少体积
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,圆锥 中,
中, 为底面圆的两条直径 ,AB交CD于O,且
为底面圆的两条直径 ,AB交CD于O,且 ,
, ,
, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求圆锥 的表面积;求圆锥
的表面积;求圆锥 的体积。
的体积。
(3)求异面直线 与
与 所成角的正切值 .
所成角的正切值 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图所示,在直棱柱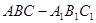 中,
中,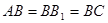 ,
,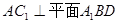 ,
,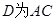 的中点.
的中点.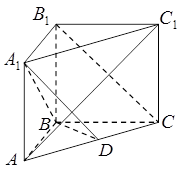
(1)求证: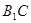 ∥
∥ ;
;
(2)求证: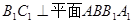 ;
;
(3)在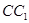 上是否存在一点
上是否存在一点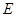 ,使得
,使得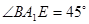 ,若存在,试确定
,若存在,试确定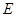 的位置,并判断
的位置,并判断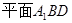 与平面
与平面 是否垂直?若不存在,请说明理由.
是否垂直?若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分) 如图,四边形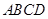 中,
中, 为正三角形,
为正三角形,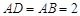 ,
,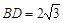 ,
,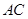 与
与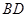 交于
交于 点.将
点.将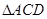 沿边
沿边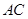 折起,使
折起,使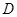 点至
点至 点,已知
点,已知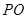 与平面
与平面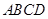 所成的角为
所成的角为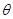 ,且
,且 点在平面
点在平面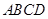 内的射影落在
内的射影落在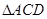 内.
内.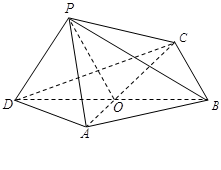
(Ⅰ)求证: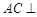 平面
平面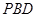 ;
;
(Ⅱ)若已知二面角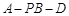 的余弦值为
的余弦值为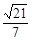 ,求
,求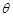 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com