【题目】已知椭圆
：
的焦点分别为
，
，椭圆的离心率为
，且经过点
，经过，作平行直线
，
，交椭圆于两点
，
和两点
，
.
（1）求的方程；
（2）求四边形
面积的最大值.
【答案】（1）
（2）四边形
面积最大值为6
【解析】
（1）利用离心率求得
关系，再将点坐标代入椭圆方程求得即可；
（2）
斜率存在时，设出方程
，与椭圆方程联立，利用根与系数关系表示出
，又因为
之间的距离就是
到直线：
的距离，可得关系式，表示出
，求出S的范围；斜率不存在时，求出四边形的面积，综合可得面积最大值．
解：（1）由
，
得
，又
，
解得：
，
，
所以
的方程为：.
（2）当直线的斜率存在时，
设斜率为
，设
，
，又
，
所以直线的方程为，
由
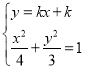，得
，
∴
，
，
∴
.
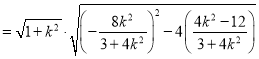
又，
之间的距离即为
到直线：的距离：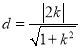
，
∴四边形面积为：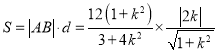
，
设
，
则四边形面积为：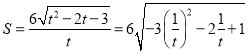
，
∵
，
∴
，
∴
.
当直线的斜率不存在时，四边形面积为：
，
所以四边形面积
，
因此四边形面积最大值为6.
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案科目：高中数学 来源： 题型：
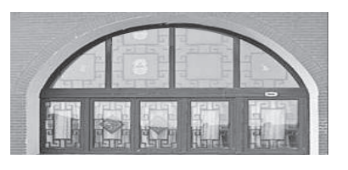
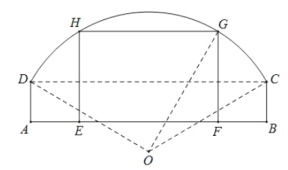
【题目】如下图所示，某窑洞窗口形状上部是圆弧
，下部是一个矩形
，圆弧所在圆的圆心为O，经测量
米，
米，
，现根据需要把此窑洞窗口形状改造为矩形
，其中E，F在边
上，G，H在圆弧上.设
，矩形的面积为S.
（1）求矩形的面积S关于变量
的函数关系式；
（2）求
为何值时，矩形的面积S最大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，已知曲线
的参数方程为
（
为参数）。曲线
的参数方程为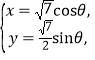
（
为参数），在以坐标原点为极点，
轴正半轴为极轴建立极坐标系.
（1）求曲线，的极坐标方程；
（2）在极坐标系中，射线
与曲线交于点
，射线
与曲线交于点
，求
的面积（其中
为坐标原点）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《中华人民共和国道路交通安全法》第47条的相关规定：机动车行经人行横道时，应当减速慢行；遇行人正在通过人行横道，应当停车让行，俗称“礼让斑马线”，《中华人民共和国道路交通安全法》第90条规定：对不礼让行人的驾驶员处以扣3分，罚款50元的处罚．
（1）交警从这5个月内通过该路口的驾驶员中随机抽查了50人，调查驾驶员不“礼让斑马线”行为与驾龄的关系，得到如下列联表：能否据此判断有97.5%的把握认为“礼让斑马线”行为与驾龄有关？
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
（2）下图是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为的折线图：
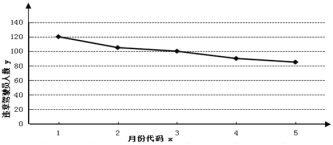
请结合图形和所给数据求违章驾驶员人数y与月份x之间的回归直线方程
，并预测该路口7月份的不“礼让斑马线”违章驾驶员人数．
附注：参考数据：
，
．
参考公式：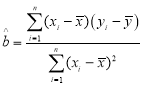
，
，
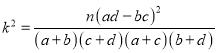（其中
）
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的方程为
，其焦点为
，
为过焦点的抛物线的弦，过
分别作抛物线的切线
，
，设，相交于点
．
（1）求
的值；
（2）如果圆
的方程为
，且点在圆内部，设直线与相交于
，
两点，求
的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
