
����Ŀ��ij���ڿ�չ������ȫ��������������У�����������ʵ����Ч�����������dz��л���������Ϊ�Ĺۣ�����������.�������������У�ij��վ�Ƴ��˹��ڻ��������ͱ�������������ʾ����飬�ִӲ����ʾ��������Ⱥ�����ѡ��200�ˣ�������200�˰�������飺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ����5��
����5��![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
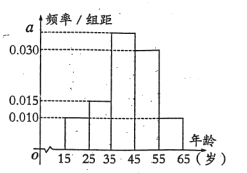
��1�����a��ֵ��
��2�����Ѵ������С�ĵ�1��2�����÷ֲ�����ķ�����ȡ5�ˣ���Ҫ�ٴ���5���������ȡ3�˽����ʾ����飬���2��鵽![]() �ˣ����������
�ˣ����������![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() .
.
���𰸡���1��![]() ��2���������
��2���������
��������
��1����Ƶ�ʷֲ�ֱ��ͼ�����ʣ������![]() ��ֵ��
��ֵ��
��2�����ݷֲ�����Ĺ��������������������������![]() �����п���ȡֵΪ1��2��3���ֱ��������ʣ��г��ֲ��м����������.
�����п���ȡֵΪ1��2��3���ֱ��������ʣ��г��ֲ��м����������.
�⣺��1����![]() �����
�����![]() .
.
��2����1��2��������ֱ�Ϊ20�ˣ�30�ˣ��ӵ�1��2�����÷ֲ�����ķ�����ȡ5�ˣ����1��2���ȡ����������Ϊ2�ˣ�3��.
�������![]() �����п���ȡֵΪ1��2��3.����
�����п���ȡֵΪ1��2��3.����
![]() ��
��![]() ��
��![]() ��
��
�����������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| l | 2 | 3 |
P |
|
|
|
![]()


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��Բ
�У���֪��Բ![]() ����Ϊ
����Ϊ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ��
��![]() ��
��![]() Ϊ��Բ
Ϊ��Բ![]() �����㣬Բ
�����㣬Բ![]() .
.
��1����![]() �ᣬ������ֱ��
�ᣬ������ֱ��![]() ��Բ
��Բ![]() ���У���Բ
���У���Բ![]() �ķ��̣�
�ķ��̣�
��2����Բ![]() �İ뾶Ϊ2����
�İ뾶Ϊ2����![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() ��Բ
��Բ![]() �ص��ҳ������ֵ.
�ص��ҳ������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .����
.����![]() ��
��
��1����![]() .��֤��
.��֤��![]() .
.
��2��������ʽ![]() ��
��![]() �����������
�����������![]() ��ȡֵ��Χ
��ȡֵ��Χ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �����Ҷ���ֱ�ΪA��B��������Ϊ
�����Ҷ���ֱ�ΪA��B��������Ϊ![]() �����᳤Ϊ4������S��C��λ��x���Ϸ���ֱ��
�����᳤Ϊ4������S��C��λ��x���Ϸ���ֱ��![]() ��ֱ��
��ֱ��![]() ���ֱ���M��N����.
���ֱ���M��N����.
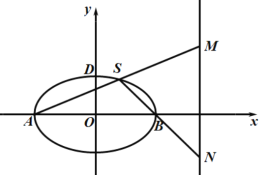
��1������ԲC�ķ���
��2����|MN|����Сֵ
��3����![]() ��Сʱ������ԲC���Ƿ���������ĵ�T��ʹ��TSB���Ϊ
��Сʱ������ԲC���Ƿ���������ĵ�T��ʹ��TSB���Ϊ![]() �������ڣ���ȷ����T�ĸ������������ڣ���˵������
�������ڣ���ȷ����T�ĸ������������ڣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ȳ�����{an}��ǰn���ΪSn����a3+2S6��77��a10��a5��10.
��1��������{an}��ͨ�ʽ��
��2������{bn}���㣺b1��1��bn��bn��1��an��n+1��n��2����������{![]() }��ǰn���Tn.
}��ǰn���Tn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ι�������Ϊ��������26�����ξ���ķ����������Ը���26�����ξ���Ľ�ͨ����ȫ����������������������ָ��������֣�ÿ��������ͷ�0�֣���߷�100�֣�ÿ�������ܷ�Ϊ������÷�֮�ͣ����ݿ������ֽ�������ƽ�ͨ�÷��밲ȫ�÷�ɢ��ͼ����ͨ�÷��뾰���ܷ�ɢ��ͼ���£�
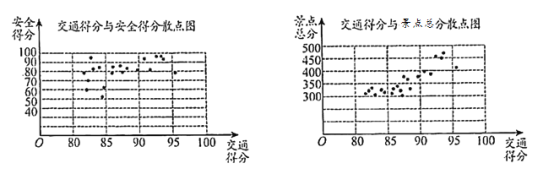
�����ͼ�����ṩ����Ϣ������������⣺
��I�����ӽ�ͨ�÷�ǰ6���ľ�������ȡ2�������䰲ȫ�÷ֶ�����90�ֵĸ��ʣ�
��II�����Ӿ����ܷ�����ǰ6���ľ�������ȡ3�����ǰ�ȫ�÷ֲ�����90�ֵľ������Ϊ![]() �����������
�����������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��III���Ǹ���26������Ľ�ͨƽ���÷�Ϊ![]() ��ȫƽ���÷�Ϊ
��ȫƽ���÷�Ϊ![]() ��д��
���![]() ��
��![]() �Ĵ�С��ϵ����ֻд�������
�Ĵ�С��ϵ����ֻд�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�Ķ���A��B��C�ֱ���������ֱ����������OX��OY��OZ�ϣ��������������У������Ϊ���� ����
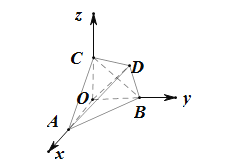
A.O��ABC��������B.�����D��OB��A��ƽ���Ϊ![]()
C.ֱ��AD��ֱ��OB���ɽ�Ϊ![]() D.ֱ��OD��ƽ��ABC
D.ֱ��OD��ƽ��ABC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���Բ![]() ���ҽ��㡢�Ҷ���ֱ�ΪF��A����ԭ���ֱ������ԲC���ڵ�P��Q����P�ڵ�һ�����ڣ�������PA��QF����
���ҽ��㡢�Ҷ���ֱ�ΪF��A����ԭ���ֱ������ԲC���ڵ�P��Q����P�ڵ�һ�����ڣ�������PA��QF����![]() ��
��![]() �������
�������![]() �����3����
�����3����
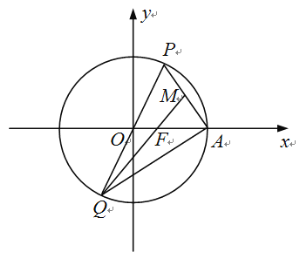
��1������ԲC�ı����̣�
��2����֪MΪ�߶�PA���е㣬����QA��QM��
����֤��Q��F��M���㹲�ߣ�
�ڼ�ֱ��QP��QM��QA��б�ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰ
��ǰ![]() ���
���![]() ����
����![]() ��
��![]() ��
��![]() ������
������![]() ����
����![]() ����
����![]() ��
��![]() ��������������
��������������![]() ��ʹ��
��ʹ��![]() ����������
����������![]() ������Ϊ2������Ϊ
������Ϊ2������Ϊ![]() �ĵȲ����У�
�ĵȲ����У�![]() Ϊ��ǰ
Ϊ��ǰ![]() ��ͣ������½�����ȷ���ǣ� ��
��ͣ������½�����ȷ���ǣ� ��
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com