
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为
为![]() 的准线与
的准线与![]() 轴的交点,点
轴的交点,点![]() 在抛物线
在抛物线![]() 上,设
上,设![]() ,
,![]() ,
,![]() ,有以下
,有以下![]() 个结论:
个结论:
①![]() 的最大值是
的最大值是![]() ;②
;②![]() ;③存在点
;③存在点![]() ,满足
,满足![]() .
.
其中正确结论的序号是______.
【答案】①②③
【解析】
由直线![]() 与抛物线相切可求得
与抛物线相切可求得![]() 的最大值,可判断命题①的正误;利用弦化切的思想和正弦定理边角互化思想可判断命题②的正误;由
的最大值,可判断命题①的正误;利用弦化切的思想和正弦定理边角互化思想可判断命题②的正误;由![]() 结合
结合![]() 化简得出
化简得出![]() ,判断该方程在
,判断该方程在![]() 时是否有根,由此可判断命题③的正误,综合可得出结论.
时是否有根,由此可判断命题③的正误,综合可得出结论.
如下图所示:
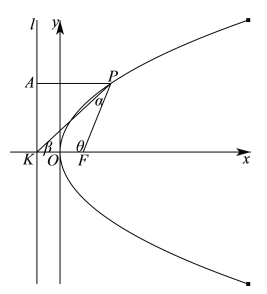
易知点![]() ,可设直线
,可设直线![]() 的方程为
的方程为![]() ,
,
由图形可知,当直线![]() 与抛物线相切时,
与抛物线相切时,![]() 取最大值,
取最大值,
联立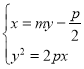 ,消去
,消去![]() 得
得![]() ,
,![]() ,得
,得![]() ,
,
此时,直线![]() 的斜率为
的斜率为![]() ,所以,
,所以,![]() 的最大值为
的最大值为![]() ,命题①正确;
,命题①正确;
过点![]() 作抛物线准线
作抛物线准线![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,则
,则![]() ,
,
由抛物线的定义可知![]() ,则
,则![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,所以
,所以![]() ,命题②正确;
,命题②正确;
若存在点![]() ,使得
,使得![]() ,则
,则![]() ,可得
,可得![]() ,则
,则![]() .
.
由②知![]()
即![]() ,
,
![]() ,则
,则![]() ,
,
构造函数![]() ,则
,则![]() ,
,![]() ,
,
由零点存在定理可知,函数![]() 在区间
在区间![]() 上有零点,
上有零点,
所以,关于![]() 的方程
的方程![]() 在
在![]() 时有实数解,命题③正确.
时有实数解,命题③正确.
因此,正确结论的序号为①②③.
故答案为:①②③.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.

(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值.金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,顶端剥落10米,则胡夫金字塔现高大约为( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点是椭圆
的顶点是椭圆![]() 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.
(1)求抛物线![]() 的方程;
的方程;
(2)已知动直线![]() 过点
过点![]() ,交抛物线
,交抛物线![]() 于
于![]() ,
,![]() 两点,坐标原点
两点,坐标原点![]() 为
为![]() 的中点,求证
的中点,求证![]() ;
;
(3)在(2)的条件下,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆所截得的弦长恒为定值?如果存在,求出
为直径的圆所截得的弦长恒为定值?如果存在,求出![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线![]() 的焦点相同.直线
的焦点相同.直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的一个方向向量为
的一个方向向量为![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点);
为坐标原点);
(3)试问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
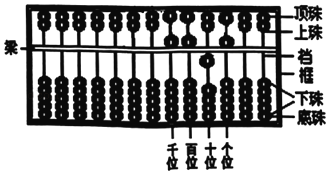
【题目】珠算被誉为中国的第五大发明,最早见于汉朝徐岳撰写的《数术记遗》2013年联合国教科文组织正式将中国珠算项目列入教科文组织人类非物质文化遗产.如图,我国传统算盘每一档为两粒上珠,五粒下珠,也称为“七珠算盘”.未记数(或表示零)时,每档的各珠位置均与图中最左档一样;记数时,要拨珠靠梁,一个上珠表示“5”,一个下珠表示“1”,例如:当千位档一个上珠、百位档一个上珠、十位档一个下珠、个位档一个上珠分别靠梁时,所表示的数是5515.现选定“个位档”、“十位档”、“百位档”和“千位档”,若规定每档拨动一珠靠梁(其它各珠不动),则在其可能表示的所有四位数中随机取一个数,这个数能被3整除的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() ,左顶点为A,过点A的直线l与C交于另一个点M,且与直线x=t交于点N.
,左顶点为A,过点A的直线l与C交于另一个点M,且与直线x=t交于点N.
(1)求椭圆C的方程;
(2)是否存在实数t,使得![]() 为定值?若存在,求实数t的值;若不存在,请说明理由.
为定值?若存在,求实数t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆M:![]() 经过圆N:
经过圆N:![]() 与x轴的两个交点和与y轴正半轴的交点.
与x轴的两个交点和与y轴正半轴的交点.

(1)求椭圆M的方程;
(2)若点P为椭圆M上的动点,点Q为圆N上的动点,求线段PQ长的最大值;
(3)若不平行于坐标轴的直线交椭圆M于A、B两点,交圆N于C、D两点,且满足![]() 求证:线段AB的中点E在定直线上.
求证:线段AB的中点E在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com