Question

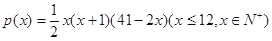某商场预计2014年从1月起前个月顾客对某种商品的需求总量（单位：件）
（1）写出第个月的需求量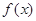的表达式；
（2）若第个月的销售量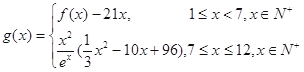（单位：件），每件利润（单位：元），求该商场销售该商品，预计第几个月的月利润达到最大值？月利润的最大值是多少？（参考数据：）

Answer 1

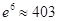(1) f(x)= 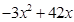.;(2) .第6个月时最大利润为3000元

解析试题分析：(1)利用数列求和的递推思想可得第x个月的需求量.
（2）由（1）可得第x个月的需求量.根据利润计算公式求得月利润.利用分段函数的范围求出各段利润的最大值.最大值的求解是通过求导的知识.本题属于应用题的问题，阅读理解题意要细心.其中涉及求和的问题，有涉及第几个月的问题，及是数列中的通项与求和关系.另外通过分段的求导在对比出最大值.
试题解析：（1）时，f(x)="p(x)-p(x-1)=" 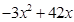.x=1时p(x)=39也满足所以f(x)= ..
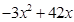(2)设该商场第x个月的月利润为w（元）.则①且时.w(x)= ..由.得x=6.所以w(x)在[1,6]上递增，在[6,7)上递减.所以.②且时=1000..所以w(x)在[7,8]上递增，在（8,12]上递减.所以.综上.第6个月时最大利润为3000元.
考点：1.数列的通项问题.2.导数求最值问题.3.分段函数问题.