
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在其定义域内存在实数
,若在其定义域内存在实数![]() 满足
满足![]() ,则称函数
,则称函数![]() 为“局部奇函数”,若函数
为“局部奇函数”,若函数![]() 是定义在
是定义在![]() 上的“局部奇函数”,则实数
上的“局部奇函数”,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ( x R ,且 e 为自然对数的底数).
( x R ,且 e 为自然对数的底数).
⑴ 判断函数 f x 的单调性与奇偶性;
⑵是否存在实数 t ,使不等式![]() 对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第二届乌镇互联网大会中, 为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在![]() 、
、![]() 、
、![]() 三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
A.![]() 种B.
种B.![]() 种
种
C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 平面上有一点列
平面上有一点列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,对每个正整数
,对每个正整数![]() ,点
,点![]() 位于函数
位于函数![]()
![]() 的图像上,且点
的图像上,且点![]() 、点
、点![]() 与点
与点![]() 构成一个以
构成一个以![]() 为顶角顶点的等腰三角形;
为顶角顶点的等腰三角形;
(1)求点![]() 的纵坐标
的纵坐标![]() 的表达式;
的表达式;
(2)若对每个自然数![]() ,以
,以![]() 、
、![]() 、
、![]() 为边长能构成一个三角形,求
为边长能构成一个三角形,求![]() 的取值范围;
的取值范围;
(3)设![]()
![]() ,若
,若![]() 取(2)中确定的范围内的最小整数,问数列
取(2)中确定的范围内的最小整数,问数列![]() 的最大项的项数是多少?试说明理由;
的最大项的项数是多少?试说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校冬季长跑活动中,学校要给获得一二等奖的学生购买奖品,要求花费总额不得超过200元.已知一等奖和二等奖奖品的单架分别为20元10元,一等奖人数与二等奖人数的比值不得高于![]() ,且获得一等奖的人数不能少于2人,有下列四个结论:①最多可以购买4份一等奖奖品②最多可以购买16份二等奖奖品③购买奖品至少要花费100元④共有20种不同的购买奖品方案其中正确结论的序号为___________.
,且获得一等奖的人数不能少于2人,有下列四个结论:①最多可以购买4份一等奖奖品②最多可以购买16份二等奖奖品③购买奖品至少要花费100元④共有20种不同的购买奖品方案其中正确结论的序号为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校计划面向高一年级![]() 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了![]() 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有![]() 人.在这
人.在这![]() 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为![]() 人.
人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的![]() 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过![]() 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: 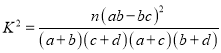 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com