
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相同数字的概率;
(Ⅱ)求取出的两个球上标号之积能被3整除的概率.
【答案】(1) ![]() . (2)
. (2) ![]() .
.
【解析】
设从甲、乙两个盒子中各取1个球,其数字分别为x,y.
用(x,y)表示抽取结果,则所有可能的结果有16种,即
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4).
(1)设“取出的两个球上的标号相同”为事件A,
则A={(1,1),(2,2),(3,3),(4,4)}.
事件A由4个基本事件组成,故所求概率P(A)=![]() =
=![]() .
.
(2)设“取出的两个球上标号的数字之积能被3整除”为事件B,
则B={(1,3),(3,1),(2,3),(3,2),(3,3),(3,4),(4,3)}
事件B由7个基本事件组成,故所求概率P(A)=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】随着人工智能的兴起,越来越多的事物可以用机器人替代,某学校科技小组自制了一个机器人小青,共可以解决函数、解析几何、立体几何三种题型![]() 已知一套试卷共有该三种题型题目20道,小青解决一个函数题需要6分钟,解决一个解析几何题需要3分钟,解决一个立体几何题需要9分钟
已知一套试卷共有该三种题型题目20道,小青解决一个函数题需要6分钟,解决一个解析几何题需要3分钟,解决一个立体几何题需要9分钟![]() 已知小青一次开机工作时间不能超过90分钟,若答对一道函数题给8分,答对一道解析几何题给6分,答对一道立体几何题给9分
已知小青一次开机工作时间不能超过90分钟,若答对一道函数题给8分,答对一道解析几何题给6分,答对一道立体几何题给9分![]() 该兴趣小组通过合理分配题目可使小青在一次开机工作时间内做这套试卷得分最高,则最高得分为______分
该兴趣小组通过合理分配题目可使小青在一次开机工作时间内做这套试卷得分最高,则最高得分为______分![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内的定点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() ,动圆
,动圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .在曲线
.在曲线![]() 上任取一点
上任取一点![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
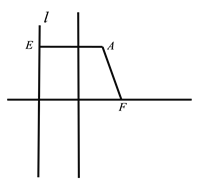
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)判断![]() 的平分线所在的直线与曲线的交点个数,并说明理由.
的平分线所在的直线与曲线的交点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动.小明收集班内20名同学今年春节期间抢到红包金额![]() (元)如下(四舍五入取整数):
(元)如下(四舍五入取整数):
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
对这20个数据进行分组,各组的频数如下:

(Ⅰ)写出m,n的值,并回答这20名同学抢到的红包金额的中位数落在哪个组别;
(Ⅱ)记C组红包金额的平均数与方差分别为![]() 、
、![]() ,E组红包金额的平均数与方差分别为
,E组红包金额的平均数与方差分别为![]() 、
、![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从A,E两组所有数据中任取2个,求这2个数据差的绝对值大于100的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵.将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,则阳马
,则阳马![]() 的外接球的表面积是( )
的外接球的表面积是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/30/1913191114645504/1914064210190336/STEM/70d44ba6321c44a9bcc99e6010bf5643.png]
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点 ,且两个焦点的坐标分别为
,且两个焦点的坐标分别为![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 上的三个不同的点,
上的三个不同的点, ![]() 为坐标原点,且
为坐标原点,且![]() ,求证:四边形
,求证:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com