
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为1,2,3,…,
为1,2,3,…,![]() 的一个排列,若
的一个排列,若![]() 互不相同,则称数列
互不相同,则称数列![]() 具有性质
具有性质![]() .
.
(1)若![]() ,且
,且![]() ,写出具有性质
,写出具有性质![]() 的所有数列
的所有数列![]() ;
;
(2)若数列![]() 具有性质
具有性质![]() ,证明:
,证明:![]() ;
;
(3)当![]() 时,分别判断是否存在具有性质
时,分别判断是否存在具有性质![]() 的数列
的数列![]() ?请说明理由.
?请说明理由.
【答案】(1)![]() 或
或![]() ;(2)证明见详解;(3)
;(2)证明见详解;(3)![]() 时不存在,
时不存在,![]() 时存在,理由见详解
时存在,理由见详解
【解析】
(1)根据题意直接写数列即可;
(2)假设![]() ,则
,则![]() ,那么
,那么![]() 最多有
最多有![]() 个结果,无法满足
个结果,无法满足![]() 个
个![]() 互不相同,故不满足性质
互不相同,故不满足性质![]() ,题设得证;
,题设得证;
(3)根据两组1,2,3,…,![]() 中的奇偶个数,可以推导
中的奇偶个数,可以推导![]() 的结果中,奇数与偶数的个数组合,从而得出结论.
的结果中,奇数与偶数的个数组合,从而得出结论.
(1)若![]() ,且
,且![]() ,
,
则具有性质![]() 的数列
的数列![]() 有两个,
有两个,
分别是![]() 或
或![]() ;
;
(2)数列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为1,2,3,…,
为1,2,3,…,![]() 的一个排列,
的一个排列,
则![]() 最多有
最多有![]() 个结果,分别是
个结果,分别是![]() ,
,
若![]() ,则
,则![]() ,
,
![]() 时,
时,![]() 最多有
最多有![]() 个结果,分别是
个结果,分别是![]() ,
,
因此,若![]() ,则
,则![]() 最多有
最多有![]() 个结果,分别是
个结果,分别是![]() ,
,
无法满足![]() 个
个![]() 互不相同,故不满足性质
互不相同,故不满足性质![]() ,
,
因此,若数列![]() 具有性质
具有性质![]() ,则
,则![]() ;
;
(3)当![]() 时,不存在具有性质
时,不存在具有性质![]() 的数列
的数列![]() ;
;
当![]() 时,存在具有性质
时,存在具有性质![]() 的数列
的数列![]() .
.
证明如下:
当![]() 时,
时,![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为1,2,3,…,7的一个排列,
为1,2,3,…,7的一个排列,
若其具有性质![]() ,则
,则![]() 的结果应该分别是
的结果应该分别是![]() ,
,
包含3个奇数,4个偶数,
而两组1,2,3,…,7中,包含8个奇数,6个偶数,
其中,3个奇数与3个偶数相减能得到结果中的3个奇数,
但剩下的5个奇数和3个偶数组合无法减出4个偶数,
因此![]() 时,不存在具有性质
时,不存在具有性质![]() 的数列
的数列![]() ;
;
若![]() ,则两组1,2,3,…,8中包含8个奇数,8个偶数,
,则两组1,2,3,…,8中包含8个奇数,8个偶数,
可以组合相减得到![]() ,这4个偶数,4个奇数,
,这4个偶数,4个奇数,
因此![]() 时,存在具有性质
时,存在具有性质![]() 的数列
的数列![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】近年来,在新高考改革中,打破文理分科的“![]() ”模式初露端倪,其中语、数、外三门课为必考科目,剩下三门为选考科目选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分,假定
”模式初露端倪,其中语、数、外三门课为必考科目,剩下三门为选考科目选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分,假定![]() 省规定:选考科目按考生成绩从高到低排列,按照占总体
省规定:选考科目按考生成绩从高到低排列,按照占总体![]() 、
、![]() 、
、![]() 、
、![]() 分别赋分
分别赋分![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,为了让学生们体验“赋分制”计算成绩的方法,
分,为了让学生们体验“赋分制”计算成绩的方法,![]() 省某高中高一(
省某高中高一(![]() )班(共
)班(共![]() 人)举行了以此摸底考试(选考科目全考,单料全班排名),知这次摸底考试中的物理成绩(满分
人)举行了以此摸底考试(选考科目全考,单料全班排名),知这次摸底考试中的物理成绩(满分![]() 分)频率分布直方图,化学成绩(满分
分)频率分布直方图,化学成绩(满分![]() 分)茎叶图如图所示,小明同学在这次考试中物理
分)茎叶图如图所示,小明同学在这次考试中物理![]() 分,化学
分,化学![]() 多分.
多分.
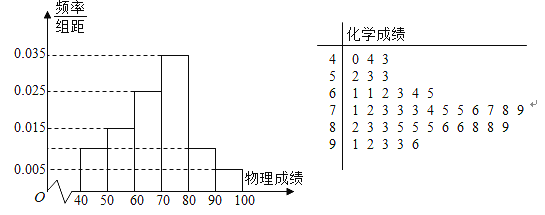
(1)采用赋分制后,求小明物理成绩的最后得分;
(2)若小明的化学成绩最后得分为![]() 分,求小明的原始成绩的可能值;
分,求小明的原始成绩的可能值;
(3)若小明必选物理,其他两科从化学、生物、历史、地理、政治五科中任选,求小明此次考试选考科目包括化学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为:
的方程为:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为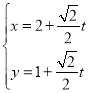 (
(![]() 为参数).
为参数).
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某批次的某种灯泡中,随机地抽取![]() 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命(天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)根据频率分布表中的数据,写出![]() 、
、![]() 的值;
的值;
(2)某人从灯泡样品中随机地购买了![]() 个,如果这
个,如果这![]() 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求![]() 的最小值;
的最小值;
(3)某人从这个批次的灯泡中随机地购买了![]() 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用![]() 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面坐标系中![]() 中,已知直线l的参考方程为
中,已知直线l的参考方程为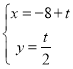 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为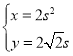 (s为参数).设P为曲线C上的动点,
(s为参数).设P为曲线C上的动点,
(Ⅰ)求直线l和曲线C的直角坐标方程;
(Ⅱ)求点P到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
(1)求实数k的值,并讨论函数f(x)的单调性;
(2)设函数g(x)![]() ,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位置分别记为点
大道上嬉戏,所在位置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的2倍,且
,乙丙之间的距离是甲乙之间距离的2倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为θ的函数,并求甲乙之间的最小距离.
表示为θ的函数,并求甲乙之间的最小距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com